Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm \[{\rm{A}}\]và \[{\rm{B}}\] dao động điều hòa cùng pha theo phương thẳng đứng tạo ra hai sóng kết hợp có bước sóng 4 cm. Khoảng cách giữa hai nguồn là AB = 30 cm. M là điểm ở mặt nước nằm ngoài hình tròn đường kính AB là cực đại giao thoa cùng pha với nguồn. H là trung điểm của AB. Độ dài ngắn nhất của đoạn MH gần nhất với giá trị nào sau đây?
Quảng cáo
Trả lời:
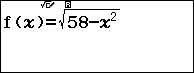
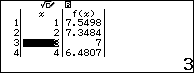 (thỏa mãn)
(thỏa mãn)Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Câu 2
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.