Một vật dao động điều hoà theo phương trình x = 5cos(2πt - π/2) cm. Kể từ lúc t = 0, quãng đường vật đi được sau 12,375 s bằng
Câu hỏi trong đề: 2020 câu Trắc nghiệm tổng hợp Vật lí 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Tại thời điểm ban đầu vật xuất phát từ VTCB đi theo chiều dương.
Chu kì dao động \(T = \frac{{2\pi }}{\omega } = 1\left( s \right)\)
Xét khoảng thời gian \(t = 12,375 = 12T + \frac{{3T}}{8}\)
Như vậy quãng đường đi được sẽ là s = s1 + s2
với s1 là quãng đường vật đi được trong thời gian 12T kể từ khi bắt đầu dao động, s2 là quãng đường vật đi được trong thời gian \(\frac{{3T}}{8}\) tiếp theo.
- Trong thời gian 12T, quãng đường vật đi được là s1 = 12.4A = 48A
- Trong thời gian \(\frac{{3T}}{8}\) tiếp theo, vật đi được quãng đường:
\({s_2} = A + \left( {A - \frac{{A\sqrt 2 }}{2}} \right) = 2A - \frac{{A\sqrt 2 }}{2}\)
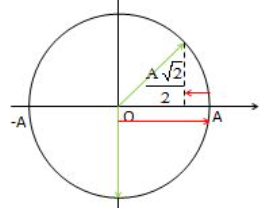
Vậy, tổng quãng đường đi được là: \(s = {s_1} + {s_2} = 48A + 2A - \frac{{A\sqrt 2 }}{2} = 50A - \frac{{A\sqrt 2 }}{2}\)
Thay số vào ta được s = 246,46 cm.
Đáp án đúng: B
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
Ta có:
\(\left\{ \begin{array}{l}{v_{max}} = \omega A\\{a_{max}} = {\omega ^2}A\end{array} \right. \Rightarrow v_{max}^2 = {\omega ^2}{A^2} \Rightarrow \frac{{v_{max}^2}}{{{a_{max}}}} = A = 4\left( {cm} \right)\)
Đáp án đúng: B
Lời giải
Lời giải
Hình chiếu của P xuống MN là H
Hệ thức lượng trong tam giác vuông:
\(P{N^2} = NH.MN \Rightarrow HN = 6,4\left( {cm} \right)\)
\(MN = MH + HN \Rightarrow HM = 3,6\left( {cm} \right)\)
Công của lực điện: \(A = qEd\)
\(A > 0\) khi điện tích chuyển động ngược chiều \(\vec E\) (do điện tích âm)
\(A < 0\) khi điện tích chuyển động cùng chiều \(\vec E\)
a. \({A_{MN}} = q.E.MN = - {4.10^{ - 8}}.200.0,1 = - {8.10^{ - 7}}\left( J \right)\)
B. \({A_{NP}} = q.E.NH = {4.10^{ - 8}}.200.0,064 = {5,12.10^{ - 7}}\left( J \right)\) (do ngược chiều điện trường)
c. \({A_{PM}} = q.E.MH = {4.10^{ - 8}}.200.0,036 = {2,88.10^{ - 7}}\left( J \right)\)(do ngược chiều điện trường)
d. A = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập