Thực hiện bài tập lớn về lập trình Python xử lí “Tam giác” với các yêu cầu sau:
Dữ liệu đầu vào: Nhập từ tệp văn bản tamgiac.txt chứa số liệu độ dài của các tam giác, mỗi dòng trong tệp văn bản chứa ba số a, b, c là số liệu về một tam giác. Độ dài các cạnh của mỗi tam giác là số nguyên hoặc số thực.
Kết quả đầu ra:
KQ1 – Phân loại tam giác: Kiểm tra ba số a, b, c có phải là độ dài ba cạnh của một tam giác hay không? Nếu ba số a, b, c là độ dài ba cạnh của một tam giác thì phân loại tam giác đó và đếm số lượng từng loại (tam giác đều, tam giác vuông cân, tam giác vuông, tam giác cân, tam giác thường). Kết quả đưa vào tệp phanloaiTG.txt.
KQ2 – Đưa vào tệp cvdtTG.txt:
a) Chu vi, diện tích các hình tam giác hợp lệ.
b) Cho biết hình tam giác nào có chu vi lớn nhất, hình tam giác nào có diện tích lớn nhất.
c) Sắp xếp tăng dần theo diện tích của từng loại tam giác.
Yêu cầu kết quả:
Với mục đích luyện kĩ năng lập trình, mỗi nhóm cần hoàn thành hai sản phẩm chương trình SP#1 và SP#2 với yêu cầu như sau:
SP#1: Tự viết các hàm (mô đun) chương trình, kế thừa những kết quả lập trình đã có được đến nay.
SP#2: Sử dụng tối đa các hàm đã có sẵn trong Python để hoàn thành nhiệm vụ.
Thực hiện bài tập lớn về lập trình Python xử lí “Tam giác” với các yêu cầu sau:
Dữ liệu đầu vào: Nhập từ tệp văn bản tamgiac.txt chứa số liệu độ dài của các tam giác, mỗi dòng trong tệp văn bản chứa ba số a, b, c là số liệu về một tam giác. Độ dài các cạnh của mỗi tam giác là số nguyên hoặc số thực.
Kết quả đầu ra:
KQ1 – Phân loại tam giác: Kiểm tra ba số a, b, c có phải là độ dài ba cạnh của một tam giác hay không? Nếu ba số a, b, c là độ dài ba cạnh của một tam giác thì phân loại tam giác đó và đếm số lượng từng loại (tam giác đều, tam giác vuông cân, tam giác vuông, tam giác cân, tam giác thường). Kết quả đưa vào tệp phanloaiTG.txt.
KQ2 – Đưa vào tệp cvdtTG.txt:
a) Chu vi, diện tích các hình tam giác hợp lệ.
b) Cho biết hình tam giác nào có chu vi lớn nhất, hình tam giác nào có diện tích lớn nhất.
c) Sắp xếp tăng dần theo diện tích của từng loại tam giác.
Yêu cầu kết quả:
Với mục đích luyện kĩ năng lập trình, mỗi nhóm cần hoàn thành hai sản phẩm chương trình SP#1 và SP#2 với yêu cầu như sau:
SP#1: Tự viết các hàm (mô đun) chương trình, kế thừa những kết quả lập trình đã có được đến nay.
SP#2: Sử dụng tối đa các hàm đã có sẵn trong Python để hoàn thành nhiệm vụ.
Quảng cáo
Trả lời:
A. Liệt kê các việc lớn
– Nhập vào danh sách các tam giác và lưu trữ độ dài các cạnh của chúng.
– Xây dựng logic kiểm tra tính hợp lệ của ba cạnh tam giác. Nếu ba cạnh hợp lệ, em phân loại tam giác đó để có KQ1. Đồng thời, em lưu trữ các tam giác hợp lệ cùng chỉ số trên danh sách gốc để chuyển sang bước sau. – Dùng công thức để tính chu vi, diện tích của các hình tam giác hợp lệ tìm thấy để có KQ2a.
– Với mỗi kết quả chu vi, diện tích tính được, em tìm chỉ số của hình tam giác có chu vi, diện tích lớn nhất để có KQ2b.
B. Thiết kế các hàm
1. Đọc dữ liệu từ tệp
Có thể viết hàm nhapTuTep (filename: str) đọc đầu vào từ tệp có tên
là filename.
Đầu vào: Tệp văn bản như mô tả ở bài tập.
Đầu ra: Dữ liệu trong chương trình được tổ chức như sau:
Mảng hai chiều các số liệu độ dài: Mảng n × 3, mỗi hàng chứa ba số b, c là độ dài các cạnh của một tam giác.
– Để dễ xử lí, em sắp xếp ba số a, b, c theo thứ tự tăng dần (a ≤b≤c).
def nhapTuTep (filename):
with open (file filename, mode "r") as fin:
n int (fin.readline () )
cactamgiac = []
for i in range (n) :
sides list (map (float, fin. readline ().split()))
sides.sort()
cactamgiac.append(sides)
return n, cactamgiac
2. Kiểm tra tam giác
a) Tính hợp lệ:
Em có thể tạo hàm kiemtraTamgiac(a: float, b: float, c: float) bool để kiểm tra tính hợp lệ của tam giác. Cụ thể, vì a≤b≤c nên tổng hai cạnh a + b của tam giác phải lớn hơn cạnh c, vậy a + b> c
def kiemtraTamgiac (a, b, c) -> bool: return a + b> c
b) Phân loại tam giác:
Sau khi kiểm tra tính hợp lệ, em có thể phân loại tam giác bằng cách tạo hàm: phanloai Tamgiac (a: float, b: float, c: float)-str.
– Dựa trên tên các loại: “đều”, “vuông cân”, “vuông”, “cân”, “thường”, em thấy cần phân loại dựa trên tính đều của nó trước. Vì vậy:
Trước hết, em kiểm tra tính đều của tam giác: a = b và b = c.
Sau đó, em kiểm tra tính vuông cân của tam giác: a + b = c và a = b.
Ngược lại, nếu a + b = c thì tam giác này có tính vuông.
Ngược lại, nếu a = b hoặc b = c thì tam giác này có tính cân.
a=
Ngược lại, tam giác này là tam giác thường.
Để thuận tiện cho các phần sau, em đánh số 4 loại tam giác từ 0 đến 4.

- Sau khi dựng xong hai hàm trên, em sẽ dựng hàm kq1(n, cactamgiac). Trong hàm đó, ta thực hiện như yêu cầu đề bài, đồng thời tạo ra một danh sách tam giác hợp lệ hople để lưu chỉ số các tam giác có ba cạnh hợp lệ. Sau khi in ra đáp án KQ1, ta thoát hàm và trả về danh sách hople để lưu cho việc xử lí KQ2.

c) Tính chu vi, diện tích tam giác
Viết hai hàm:


Tìm hình có chu vi lớn nhất, có diện tích lớn nhất
Viết hàm kg2 (n, cactamgiac, hople) để in ra KQ2, với hop le là chỉ số của các tam giác hợp lệ trong mảng đầu vào.
Đầu tiên, với mỗi hình hợp lệ có chỉ số x trong mảng ban đầu, ta tính chu vi, diện tích của hình cactamgiac[x]. Ta lưu vào một mảng hai chiều solieu có ba cột, cột thứ 0 là chỉ số x, cột 1 và 2 lần lượt là chu vi và diện tích của hình tam giác hợp lệ đó. Khi đó, ta có thể trả lời KQ2a ngay lúc này.
Tiếp theo, để tìm hình có chu vi, diện tích lớn nhất, ta có thể sử dụng tìm kiếm tuần tự cho mỗi câu hỏi, hoặc sắp xếp theo thứ tự giảm dần và lấy phần tử đầu tiên. Nếu dùng phương thức sort của list có thể dùng cú pháp solieu. sort(key=lambda tamgiac: tamgiac[k] ) , với k = 1 thì sắp xếp theo chu vi, với k = 2 thì sắp xếp theo diện tích. Ngay sau mỗi lượt sắp xếp, ta in ra kết quả để trả lời cho KQ2b.
Tiếp theo, ta tạo ra một danh sách lớn triList gồm 5 danh sách con có chỉ số trong triList từ 0 → 4, tương ứng với 5 loại hình tam giác khác nhau, rồi với mỗi hình tam giác hợp lệ ta đưa chúng vào danh sách có mã thích hợp.
Cuối cùng, với từng danh sách con trong triList, ta sắp xếp các hình này theo thứ tự tăng dần theo diện tích, và in ra toàn bộ mảng triList để trả lời KQ2c.



Tóm lại, đoạn code của chúng ta có dạng như sau:






Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1. Liệt kê các việc lớn
– Nhập vào danh sách các cổ vật và tham chiếu x.
– Lập công thức tính tuổi của từng cổ vật.
– Sắp xếp các cổ vật theo thứ tự tăng dần về tuổi để trả lời KQ1. – Từ tuổi của mỗi cổ vật ta xác định độ tin cậy để trả lời KQ2.
2. Thiết kế các hàm
a. Nhập vào từ tệp
Có thể viết hàm nhapTuTep ( ) để đọc dữ liệu đầu vào từ tệp covat.txt. Hàm trả về hai số n và x; cũng như hai danh sách v và m – khối lượng và số nguyên tử C của cổ vật, với v[i] và m[i] là số liệu của cổ vật thứ i.

b. Lập công thức tính tuổi của cổ vật
Ta viết hàm tinhtuoi(x, v, m),với x là mật độ nguyên tử C trong một cơ thể sống, v và m lần lượt là khối lượng và số nguyên tử C đo được của một cổ vật. Hàm sẽ trả về tuổi của cổ vật đó.
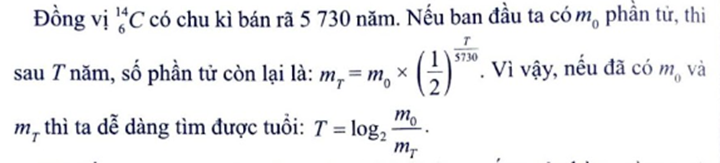
Ta thấy, mT trong trường hợp này chính là tham số m của hàm, còn m sẽ được tính bằng tích mật độ x nhân với khối lượng v. Từ đấy ta xác định tuổi của cổ vật rồi trả về kết quả.
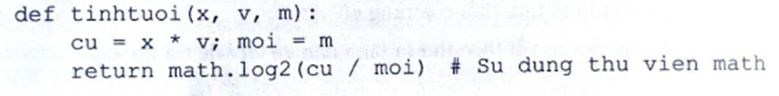
c. Sắp xếp danh sách các cổ vật các theo thứ tự niên đại
Ta viết hàm sapxep(n,v, m), với n là số lượng cổ vật và v, m là hai mảng chứa thông tin về khối lượng và số nguyên tử C đo được của các cổ vật. Ta khai báo một mảng ds hai chiều gồm 2 cột – chỉ số trong mảng gốc và tuổi của cổ vật. Để tính tuổi, ta dùng hàm tinhtuoi.
Sau đó, ta sắp xếp ds theo cột thứ hai – niên đại. Nếu dùng phương thức sort của list, có thể dùng cú pháp:

d. Kiểm tra độ tin cậy
Để không phải tính lại niên đại của cổ vật, ta sử dụng luôn mảng ds thu về từ hàm sapxep.
Vì vậy, ta có thể viết hàm danhsachtincay(ds) và trả về một mảng tincay gồm n phần tử kiểu boolean với True có nghĩa là tin cậy và False là không tin cậy.
Với mỗi cổ vật trong danh sách, ta có hai thông tin: chỉ số i của cổ vật nằm ở cột thứ nhất và tuổi niendai nằm ở cột thứ hai. Ta xem niendai có giá trị không dưới 50 000 năm hay không, nếu thoả mãn thì ta gán tincay[i] bằng True, ngược lại sẽ bằng False.
Cuối cùng, ta trả về mảng tincay để sau đó in ra câu trả lời của KQ2.

Tổng kết lại, ta có đoạn code như sau:


