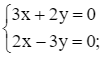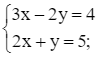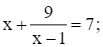Quảng cáo
Trả lời:
Giải bởi Vietjack
Bước 1. Khởi động phần mềm Geogebrra 
, chọn Complex Adaptive System (CAS).
Bước 2.
Cách 1: Ta dùng lệnh Solve ({<phương trình thứ nhất>, <phương trình thứ hai>}), {<biến số thứ nhất>, <biến số thứ hai>}), hoặc Solitions ({<phương trình thứ nhất>, <phương trình thứ hai>}), {<biến số thứ nhất>, <biến số thứ hai>}) trên ô lệnh của cửa sổ CAS để giải hệ phương trình.
Cách 2: Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.
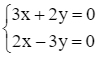
Ta nhập Solve ({3x + 2y = 0, 2x – 3y = 0}, {x, y}), ta thu được kết quả như hình vẽ.
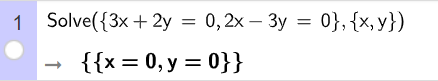
Vậy hệ phương trình đã cho có nghiệm là x = 0; y = 0.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bước 1. Khởi động phần mềm Geogebrra 
, chọn Complex Adaptive System (CAS).
Bước 2.
Cách 1: Ta dùng lệnh Solve ({<phương trình thứ nhất>, <phương trình thứ hai>}), {<biến số thứ nhất>, <biến số thứ hai>}), hoặc Solitions ({<phương trình thứ nhất>, <phương trình thứ hai>}), {<biến số thứ nhất>, <biến số thứ hai>}) trên ô lệnh của cửa sổ CAS để giải hệ phương trình.
Cách 2: Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.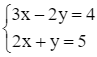 
Ta nhập Solve ({3x – 2y = 4, 2x + y = 5}, {x, y}), ta thu được kết quả như hình vẽ.
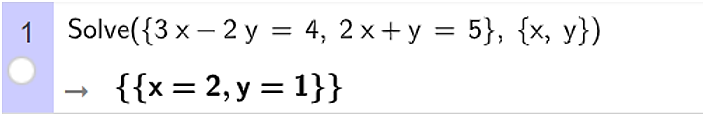
Vậy hệ phương trình đã cho có nghiệm là x = 2; y = 1.
Lời giải
Bước 1. Khởi động phần mềm Geogebrra 
, chọn Complex Adaptive System (CAS).
Bước 2. Ta dùng lệnh Solve (<phương trình>) hoặc Solitions (<phương trình>) trên ô lệnh của cửa sổ CAS để giải phương trình.
x2 – 4x + 10 = 0
Ta nhập Solve (x^2 – 4x + 10 = 0), ta thu được kết quả như hình vẽ.
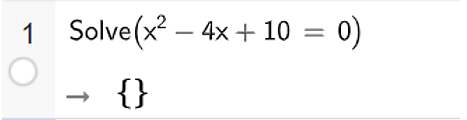
Vậy phương trình đã cho vô nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
-
Chuyên đề 8: Hình học (có đáp án)