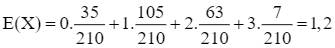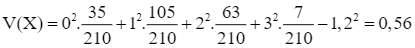Trong hộp có 12 sản phẩm, trong đó có 8 sản phẩm loại I và 4 sản phẩm loại II. Chọn ngẫu nhiên đồng thời 3 sản phẩm trong hộp. Gọi X là số sản phẩm loại I trong 3 sản phẩm được chọn ra. Tính kì vọng của biến ngẫu nhiên rời rạc X.
Quảng cáo
Trả lời:
X là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập {0; 1; 2; 3}.
Ta có ![]() .
.
+) Biến cố X = 0 là biến cố: “Không có sản phẩm loại I nào được chọn”.
Suy ra ![]() .
.
Do đó 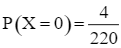 .
.
+) Biến cố X = 1 là biến cố: “Có 1 sản phẩm loại I trong 3 sản phẩm được chọn”.
Suy ra ![]() .
.
Do đó 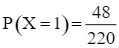 .
.
+) Biến cố X = 2 là biến cố: “Có 2 sản phẩm loại I trong 3 sản phẩm được chọn”.
Suy ra ![]() .
.
Do đó 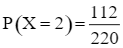 .
.
+) Biến cố X = 3 là biến cố: “Cả 3 sản phẩm được chọn đều là sản phẩm loại I”.
Suy ra ![]() .
.
Do đó 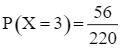 .
.
Do đó 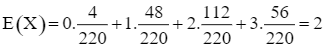 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
X là biến ngẫu nhiên rời rạc và nhận các giá trị trong tập {0; 1; 2}.
Ta có: ![]() .
.
+) Biến cố X = 0 là biến cố: “Không có học sinh nữ được chọn”.
Khi đó ![]() .
.
Do đó 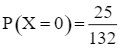 .
.
+) Biến cố X = 1 là biến cố: “Có 1 học sinh nữ trong số 2 học sinh được chọn”.
TH1: Nhóm 1 chọn được học sinh nữ, nhóm 2 chọn được học sinh nam.
Suy ra có ![]() cách chọn.
cách chọn.
TH2: Nhóm 1 chọn được học sinh nam, nhóm 2 chọn được học sinh nữ.
Suy ra có ![]() cách chọn.
cách chọn.
Do đó 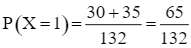 .
.
+) Biến cố X = 2 là biến cố: “Chọn được 2 học sinh nữ”.
Suy ra ![]() .
.
Do đó 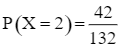 .
.
Bảng phân bố xác suất của X là:
|
X |
0 |
1 |
2 |
|
P |
|
|
|
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.