Câu hỏi:
11/07/2024 421
Giả sử một phòng thí nghiệm phải kiểm tra 120 mẫu máu người (mỗi mẫu của 1 người) để tìm ra các mẫu có chứa một loại kháng thể X. Giả sử xác suất để 1 mẫu máu có kháng thể X là 2% và các mẫu máu độc lập với nhau.
Do tính cấp bách của công tác phòng chống dịch nên thời gian dành cho xét nghiệm là rất ngắn. Thay vì xét nghiệm từng mẫu một, người ta làm như sau: Chia 120 mẫu thành 6 nhóm, mỗi nhóm có 20 mẫu. Lấy một ít máu từ mỗi mẫu trong cùng một nhóm trộn với nhau để được 1 mẫu hỗn hợp, rồi xét nghiệm mẫu hỗn hợp đó. Nếu kết quả xét nghiệm mẫu hỗn hợp là âm tính (mẫu hỗn hợp không có kháng thể X) thì coi như cả 20 mẫu trong nhóm đều không có kháng thể X, còn nếu mẫu hỗn hợp có kháng thể X, thì làm tiếp 20 xét nghiệm, mỗi xét nghiệm cho từng mẫu của nhóm.
Xác suất để một mẫu máu hỗn hợp có chứa kháng thể X là bao nhiêu?
Giả sử một phòng thí nghiệm phải kiểm tra 120 mẫu máu người (mỗi mẫu của 1 người) để tìm ra các mẫu có chứa một loại kháng thể X. Giả sử xác suất để 1 mẫu máu có kháng thể X là 2% và các mẫu máu độc lập với nhau.
Do tính cấp bách của công tác phòng chống dịch nên thời gian dành cho xét nghiệm là rất ngắn. Thay vì xét nghiệm từng mẫu một, người ta làm như sau: Chia 120 mẫu thành 6 nhóm, mỗi nhóm có 20 mẫu. Lấy một ít máu từ mỗi mẫu trong cùng một nhóm trộn với nhau để được 1 mẫu hỗn hợp, rồi xét nghiệm mẫu hỗn hợp đó. Nếu kết quả xét nghiệm mẫu hỗn hợp là âm tính (mẫu hỗn hợp không có kháng thể X) thì coi như cả 20 mẫu trong nhóm đều không có kháng thể X, còn nếu mẫu hỗn hợp có kháng thể X, thì làm tiếp 20 xét nghiệm, mỗi xét nghiệm cho từng mẫu của nhóm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta đi tính xác suất để mẫu máu hỗn hợp đó không chứa kháng thể X.
Với mỗi mẫu máu thì xác suất để không chứa kháng thể X là 1 – 0,2 = 0,98.
Xác suất để mẫu máu hỗn hợp không chứa kháng thể X là 0,9820.
Vậy xác suất để một mẫu máu hỗn hợp chứa kháng thể X là: 1 – 0,9820 ≈ 0,3324.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi X là số viên bi xanh trong 15 viên bi được chọn ra.
X là biến ngẫu nhiên rời rạc có phân bố nhị thức với tham số 15 và p = 0,6.
Ta có 
.
Vậy xác suất để có 10 viên bi xanh trong 15 viên bi được chọn ra khoảng 18,6%.
Lời giải
Gọi X là số lần xuất hiện mặt 1 chấm trong 10 lần gieo một con xúc xắc cân đối và đồng chất một cách độc lập.
X là biến ngẫu nhiên rời rạc có phân bố nhị thức với tham số 10 và 
.
Do đó 
.
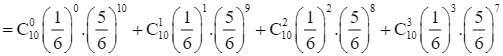
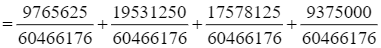
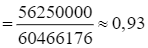Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)