Câu hỏi:
14/02/2025 474
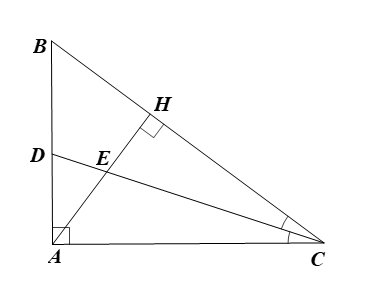
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 6{\rm{\;cm}}\) và \(AC = 8{\rm{\;cm}}.\) Kẻ đường cao \(AH.\)
a) Chứng minh
b) Tính độ dài các cạnh \(BC\) và \(AH.\)
c) Tia phân giác của \(\widehat {ACB}\) cắt \(AH\) tại \(E,\) cắt \(AB\) tại \(D.\) Chứng minh rằng \[\frac{{AC}}{{AD}} = \frac{{HC}}{{HE}}.\]
d) Tính tỉ số diện tích của \(\Delta ACD\) và \(\Delta HCE.\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 6{\rm{\;cm}}\) và \(AC = 8{\rm{\;cm}}.\) Kẻ đường cao \(AH.\)
a) Chứng minh
b) Tính độ dài các cạnh \(BC\) và \(AH.\)
c) Tia phân giác của \(\widehat {ACB}\) cắt \(AH\) tại \(E,\) cắt \(AB\) tại \(D.\) Chứng minh rằng \[\frac{{AC}}{{AD}} = \frac{{HC}}{{HE}}.\]
d) Tính tỉ số diện tích của \(\Delta ACD\) và \(\Delta HCE.\)
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) Xét \(\Delta ABC\) và \(\Delta HBA\) có: \(\widehat {BAC} = \widehat {BHA} = 90^\circ \) và \(\widehat B\) là góc chung. Do đó (g.g). b) Vì tam giác \(ABC\) vuông tại \(A,\) theo định lí Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100.\) Suy ra \(BC = 10{\rm{\;cm}}.\) |
 |
Theo câu a), nên \(\frac{{AC}}{{HA}} = \frac{{BC}}{{AB}}\) (tỉ số cạnh tương ứng).
Suy ra \(AH = \frac{{AB \cdot AC}}{{BC}} = \frac{{6 \cdot 8}}{{10}} = 4,8{\rm{\;cm}}{\rm{.}}\)
c) Xét \(\Delta ACD\) và \(\Delta HCE\) có:
\(\widehat {DAC} = \widehat {EHC} = 90^\circ \) và \(\widehat {ACD} = \widehat {HCE}\) (do \(CD\) là tia phân giác của \(\widehat {ACB}).\)
Do đó (g.g).
Suy ra \[\frac{{AC}}{{HC}} = \frac{{AD}}{{HE}}\] (tỉ số cạnh tương ứng) nên \[\frac{{AC}}{{AD}} = \frac{{HC}}{{HE}}\] (*)
d) ⦁ Chứng minh tương tự câu a), ta cũng có: (g.g).
Mà hay nên
Suy ra \[\frac{{BH}}{{AH}} = \frac{{AB}}{{CA}}\] (tỉ số cạnh tương ứng), do đó \[BH = \frac{{AB}}{{AC}} \cdot AH = \frac{6}{8} \cdot 4,8 = 3,6{\rm{\;cm}}.\]
Khi đó \[HC = BC - BH = 10 - 3,6 = 6,4{\rm{\;cm}}.\]
⦁ Ta có \(CD\) là phân giác \(\widehat {ACB}\) nên \(\frac{{CA}}{{CB}} = \frac{{DA}}{{DB}},\) do đó \[\frac{{AC}}{{AD}} = \frac{{BC}}{{BD}}.\]
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\[\frac{{AC}}{{AD}} = \frac{{BC}}{{BD}} = \frac{{AC + BC}}{{AD + BD}} = \frac{{AC + BC}}{{AB}} = \frac{{8 + 10}}{6} = 3.\]
Suy ra \(AD = \frac{{AC}}{3} = \frac{8}{3}{\rm{\;cm}}\) và \[\frac{{HC}}{{HE}} = \frac{{AC}}{{AD}} = 3.\]
Khi đó \[HE = \frac{{HC}}{3} = \frac{{6,4}}{3} = \frac{{32}}{{15}}.\]
Ta có \[\frac{{{S_{ACD}}}}{{{S_{HCE}}}} = \frac{{\frac{1}{2}AD \cdot AC}}{{\frac{1}{2}HE \cdot HC}} = \frac{{AD \cdot AC}}{{HE \cdot HC}} = \frac{{\frac{8}{3} \cdot 8}}{{\frac{{32}}{{15}} \cdot 6,4}} = \frac{{25}}{{16}}.\]
Vậy tỉ số diện tích của \(\Delta ACD\) và \(\Delta HCE\) là \[\frac{{25}}{{16}}.\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid17-1739547507.png)
Lời giải
1. Áp dụng định lí Pythagore vào tam giác \[ABH\] vuông tại \[H\], ta có:
\(A{B^2} = A{H^2} + B{H^2}\).
Suy ra \(A{H^2} = A{B^2} - B{H^2}\).
Do đó \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{{\left( {3,7} \right)}^2} - {{\left( {1,2} \right)}^2}} = 3,5\,\,(m)\).
Ta có \(\frac{{AH}}{{BH}} = \frac{{3,5}}{{1,2}} \approx 2,9\).
Mà \[2,9 > 2,2\] nên khoảng cách đặt thang cách chân tường là không an toàn.
Lời giải
a) Nửa quãng đường dài là: \(48:2 = 24\,\,{\rm{(km)}}\)
Thời gian anh Nam đi trong nửa đoạn đường đầu là: \(\frac{{24}}{x}\) (giờ)
b) Tốc độ ở nửa đoạn đường sau là: \[x - 4\] (km/giờ).
Thời gian anh Nam đi trong nửa đoạn đường sau là: \(\frac{{24}}{{x - 4}}\) (giờ)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận