Cho hình vẽ với các số liệu sau đây:
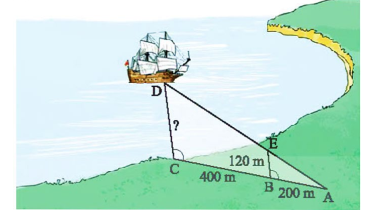
Tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C.\) (Đơn vị: m)
Cho hình vẽ với các số liệu sau đây:
Tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C.\) (Đơn vị: m)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(360\)
Ta có: \(\widehat {ACD} = \widehat {ABE}\), mà hai góc ở vị trí đồng vị nên \(CD\parallel BE.\)
Ta có: \(AC = AB + BC = 200 + 400 = 600{\rm{ }}\left( {\rm{m}} \right)\).
Theo hệ quả định lí Thalès, ta có: \(\frac{{CD}}{{BE}} = \frac{{AC}}{{AB}}.\)
Hay \(\frac{{CD}}{{120}} = \frac{{600}}{{200}}\) suy ra \(CD = \frac{{600.120}}{{200}} = 360{\rm{ }}\left( {\rm{m}} \right)\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Đồ thị hàm số \(y = ax{\rm{ }}\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua gốc tọa độ \(O\left( {0;0} \right).\)
Lời giải
Đáp án đúng là: D
Hệ số góc của đường thẳng \(y = x - 2\) là \(1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo