Câu hỏi:
06/04/2025 110
Câu 28-29. (1,0 điểm) Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3\,\,{\rm{cm}}\) và \(OB = 6\,\,{\rm{cm}}{\rm{.}}\) Trên tia đối của tia \(Ox\) lấy điểm \(C\) sao cho \(BC = 10\,\,{\rm{cm}}{\rm{.}}\) Gọi \(M\) là trung điểm của đoạn thẳng \(BC.\)
a) Tính độ dài đoạn thẳng \(OC.\)
Câu 28-29. (1,0 điểm) Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3\,\,{\rm{cm}}\) và \(OB = 6\,\,{\rm{cm}}{\rm{.}}\) Trên tia đối của tia \(Ox\) lấy điểm \(C\) sao cho \(BC = 10\,\,{\rm{cm}}{\rm{.}}\) Gọi \(M\) là trung điểm của đoạn thẳng \(BC.\)
a) Tính độ dài đoạn thẳng \(OC.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
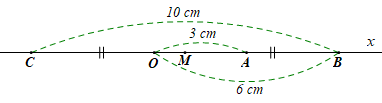
a) Ta có \(C\) nằm trên tia đối của tia \(Ox,\) điểm \(B\) nằm trên tia \(Ox\)
Do đó điểm \(O\) nằm giữa hai điểm \(C,\,\,B\)
Khi đó \(CO + OB = CB\)
Suy ra \[CO = CB - OB = 10 - 6 = 4{\rm{\;(cm)}}{\rm{.}}\]
Câu hỏi cùng đoạn
Câu 2:
b) Tính độ dài đoạn thẳng \(OM.\)
Lời giải của GV VietJack
b) • Do \(M\) là trung điểm của đoạn thẳng \(BC\) nên \(M\) nằm giữa hai điểm \(B,\,\,C\) và \(BM = MC = \frac{1}{2}BC = \frac{1}{2} \cdot 10 = 5{\rm{\;(cm)}}{\rm{.}}\)
• Do \(O\) nằm giữa hai điểm \(C,\,\,B\) và \(M\) nằm giữa hai điểm \(B,\,\,C\)
Nên \(O,\,\,M\) nằm cùng phía đối với điểm \(C.\)
Lại có \[CO < CM\] (do \[{\rm{4}}\,\,{\rm{cm}} < 5\,\,{\rm{cm}})\]
Do đó \(O\) nằm giữa hai điểm \(C,\,\,M\) nên \(CO + OM = CM\)
Suy ra \(OM = CM - CO = 5 - 4 = 1{\rm{\;(cm)}}{\rm{.}}\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: 1260.
Chiều rộng của tấm vải sau lần giặt thứ nhất là: \(270 \cdot \left( {1 - \frac{1}{{18}}} \right) = 270 \cdot \frac{{17}}{{18}} = 255{\rm{\;(cm)}}{\rm{.}}\)
Chiều dài của tấm vải sau lần giặt thứ nhất là: \(400 \cdot \left( {1 - \frac{1}{{16}}} \right) = 400 \cdot \frac{{15}}{{16}} = 375{\rm{\;(cm)}}{\rm{.}}\)
Chu vi của tấm vải là: \(2 \cdot \left( {375 + 255} \right) = 1\,\,260{\rm{\;(cm)}}{\rm{.}}\)
Câu 2
1) Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(\frac{2}{7} + \frac{5}{7} \cdot \left( {60\% - 0,25} \right) \cdot {\left( { - 2} \right)^2}.\) b) \(\frac{2}{5} \cdot \left( {\frac{{ - 5}}{{12}} + \frac{{ - 9}}{{13}}} \right) - \frac{2}{5} \cdot \left( {\frac{8}{{13}} - \frac{5}{{12}}} \right):2.\)
1) Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(\frac{2}{7} + \frac{5}{7} \cdot \left( {60\% - 0,25} \right) \cdot {\left( { - 2} \right)^2}.\) b) \(\frac{2}{5} \cdot \left( {\frac{{ - 5}}{{12}} + \frac{{ - 9}}{{13}}} \right) - \frac{2}{5} \cdot \left( {\frac{8}{{13}} - \frac{5}{{12}}} \right):2.\)
Lời giải
|
1) a) \(\frac{2}{7} + \frac{5}{7} \cdot \left( {60\% - 0,25} \right) \cdot {\left( { - 2} \right)^2}\) \( = \frac{2}{7} + \frac{5}{7} \cdot \left( {\frac{{60}}{{100}} - \frac{{25}}{{100}}} \right) \cdot 4\) \( = \frac{2}{7} + \frac{5}{7} \cdot 4 \cdot \frac{{35}}{{100}}\) \( = \frac{2}{7} + \frac{{20}}{7}.\frac{7}{{20}}\) \[ = \frac{2}{7} + 1\]\[ = \frac{9}{7}\].
|
b) \(\frac{2}{5} \cdot \left( {\frac{{ - 5}}{{12}} + \frac{{ - 9}}{{13}}} \right) - \frac{2}{5} \cdot \left( {\frac{8}{{13}} - \frac{5}{{12}}} \right):2\) \( = \frac{1}{5} \cdot 2 \cdot \left( {\frac{{ - 5}}{{12}} + \frac{{ - 9}}{{13}}} \right) - \frac{2}{5} \cdot \left( {\frac{8}{{13}} - \frac{5}{{12}}} \right) \cdot \frac{1}{2}\) \( = \frac{1}{5} \cdot \left( {\frac{{ - 10}}{{12}} + \frac{{ - 18}}{{13}}} \right) - \frac{1}{5} \cdot \left( {\frac{8}{{13}} - \frac{5}{{12}}} \right)\) \[ = \frac{1}{5} \cdot \left( {\frac{{ - 10}}{{12}} + \frac{{ - 18}}{{13}} - \frac{8}{{13}} + \frac{5}{{12}}} \right)\] \[ = \frac{1}{5} \cdot \left[ {\left( {\frac{{ - 10}}{{12}} + \frac{5}{{12}}} \right) + \left( {\frac{{ - 18}}{{13}} - \frac{8}{{13}}} \right)} \right]\] \[ = \frac{1}{5} \cdot \left( {\frac{{ - 5}}{{12}} + \frac{{ - 26}}{{13}}} \right) = \frac{1}{5} \cdot \left[ {\frac{{ - 5}}{{12}} + \left( { - 2} \right)} \right]\] \[ = \frac{1}{5} \cdot \frac{{ - 29}}{{12}} = \frac{{ - 29}}{{60}}.\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Đề thi Toán 6 Học kì 2 có đáp án (Đề 6)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 2
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)