Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại.
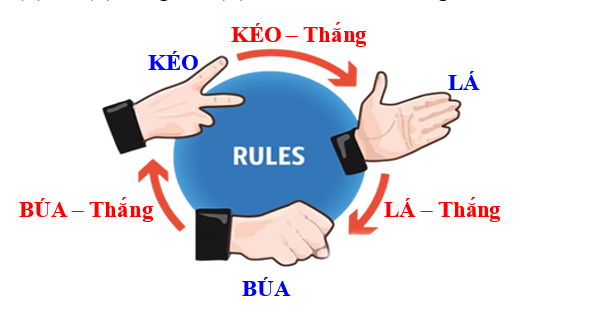
Sau đây là kết quả của mỗi ván chơi:
Lần thứ
1
2
3
4
5
6
7
8
9
10
Dũng
L
B
B
K
L
B
K
B
K
K
Nam
B
K
L
L
K
B
L
K
L
B
Tính xác suất thực nghiệm của sự kiện “Nam không thua Dũng” (kết quả viết dưới dạng số thập phân).
Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại.
Sau đây là kết quả của mỗi ván chơi:
|
Lần thứ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Dũng |
L |
B |
B |
K |
L |
B |
K |
B |
K |
K |
|
Nam |
B |
K |
L |
L |
K |
B |
L |
K |
L |
B |
Tính xác suất thực nghiệm của sự kiện “Nam không thua Dũng” (kết quả viết dưới dạng số thập phân).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp số: 0,4.
Ta có bảng thống kê sau:
|
Lần thứ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Dũng |
L |
B |
B |
K |
L |
B |
K |
B |
K |
K |
|
Nam |
B |
K |
L |
L |
K |
B |
L |
K |
L |
B |
|
Kết quả ván chơi |
Dũng thắng |
Dũng thắng |
Nam thắng |
Dũng thắng |
Nam thắng |
Hòa |
Dũng thắng |
Dũng thắng |
Dũng thắng |
Nam thắng |
Nam không thua Dũng tức là Nam thắng Dũng hoặc Nam hòa Dũng.
Trong 10 ván chơi, có 3 lần Nam thắng và 1 lần hòa nhau nên xác suất thực nghiệm của sự kiện “Nam không thua Dũng” là \(\frac{{3 + 1}}{{10}} = \frac{4}{{10}} = 0,4.\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
1) a) \[\left( {\frac{4}{5} + \frac{{ - 9}}{7}} \right):\frac{2}{3} + \left( {\frac{{ - 5}}{7} - \frac{{ - 6}}{5}} \right):\frac{2}{3}\] \[ = \left( {\frac{4}{5} + \frac{{ - 9}}{7} + \frac{{ - 5}}{7} - \frac{{ - 6}}{5}} \right):\frac{2}{3}\] \[ = \left[ {\left( {\frac{4}{5} - \frac{{ - 6}}{5}} \right) + \left( {\frac{{ - 9}}{7} + \frac{{ - 5}}{7}} \right)} \right]:\frac{2}{3}\] \[ = \left[ {\frac{{10}}{5} + \frac{{ - 14}}{7}} \right]:\frac{2}{3}\] \[ = \left[ {2 + \left( { - 2} \right)} \right]:\frac{2}{3}\] \[ = 0:\frac{2}{3} = 0.\] |
b) \(\left( { - 2,4 + \frac{1}{3}} \right):3,1 + 75\% :1\frac{1}{2}\) \[ = \left( { - \frac{{24}}{{10}} + \frac{1}{3}} \right):\frac{{31}}{{10}} + \frac{{75}}{{100}}:\frac{3}{2}\] \[ = \left( { - \frac{{12}}{5} + \frac{1}{3}} \right) \cdot \frac{{10}}{{31}} + \frac{3}{4} \cdot \frac{2}{3}\] \[ = \left( { - \frac{{36}}{{15}} + \frac{5}{{15}}} \right) \cdot \frac{{10}}{{31}} + \frac{1}{2}\] \[ = \frac{{ - 31}}{{15}} \cdot \frac{{10}}{{31}} + \frac{1}{2}\]\[ = \frac{{ - 2}}{3} + \frac{1}{2}\] \[ = \frac{{ - 4}}{6} + \frac{3}{6} = - \frac{1}{6}.\] |
Câu 2
Lời giải
Đáp án đúng là: D
Số chấm nhỏ nhất xuất hiện ở mặt phía trên khi gieo một con xúc xắc là 1. Như vậy, tổng số chấm nhỏ nhất xuất hiện ở mặt phía trên khi gieo đồng thời ba con xúc xắc là \(1 + 1 + 1 = 3 > 2.\)
Do đó sự kiện ở phương án D là chắc chắn xảy ra.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập