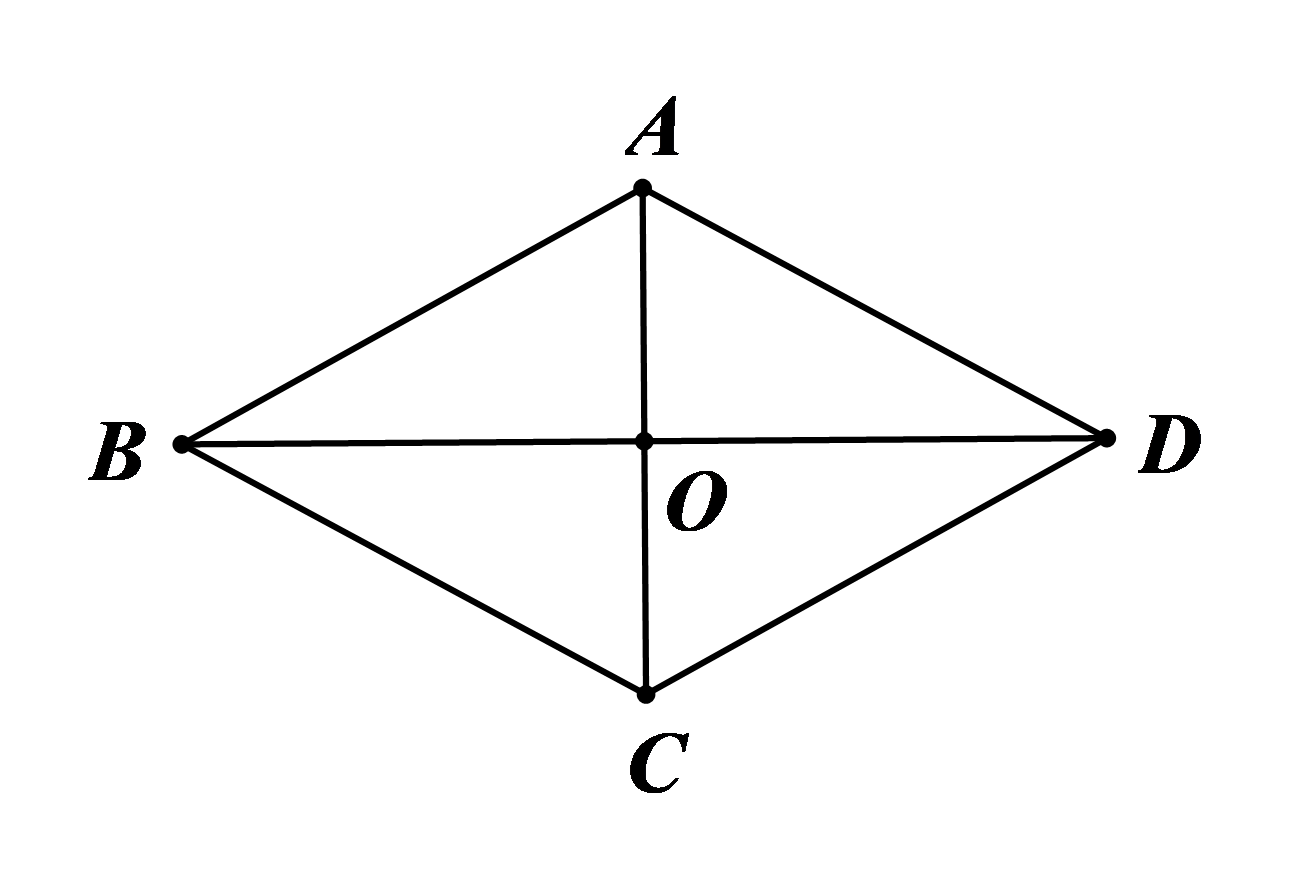Trong các hình sau:
(1) Đoạn thẳng \(AB;\)
(2) Tam giác đều \(ABC;\)
(3) Hình tròn tâm \(O;\)
(4) Hình thang cân \(ABCD\) (có đáy lớn \(CD);\)
(5) Hình thoi \(ABCD.\)
Có bao nhiêu hình vừa có trục đối xứng, vừa có tâm đối xứng?
Trong các hình sau:
(1) Đoạn thẳng \(AB;\)
(2) Tam giác đều \(ABC;\)
(3) Hình tròn tâm \(O;\)
(4) Hình thang cân \(ABCD\) (có đáy lớn \(CD);\)
(5) Hình thoi \(ABCD.\)
Có bao nhiêu hình vừa có trục đối xứng, vừa có tâm đối xứng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp số: 3.
Có 3 hình vừa có trục đối xứng, vừa có tâm đối xứng là:
|
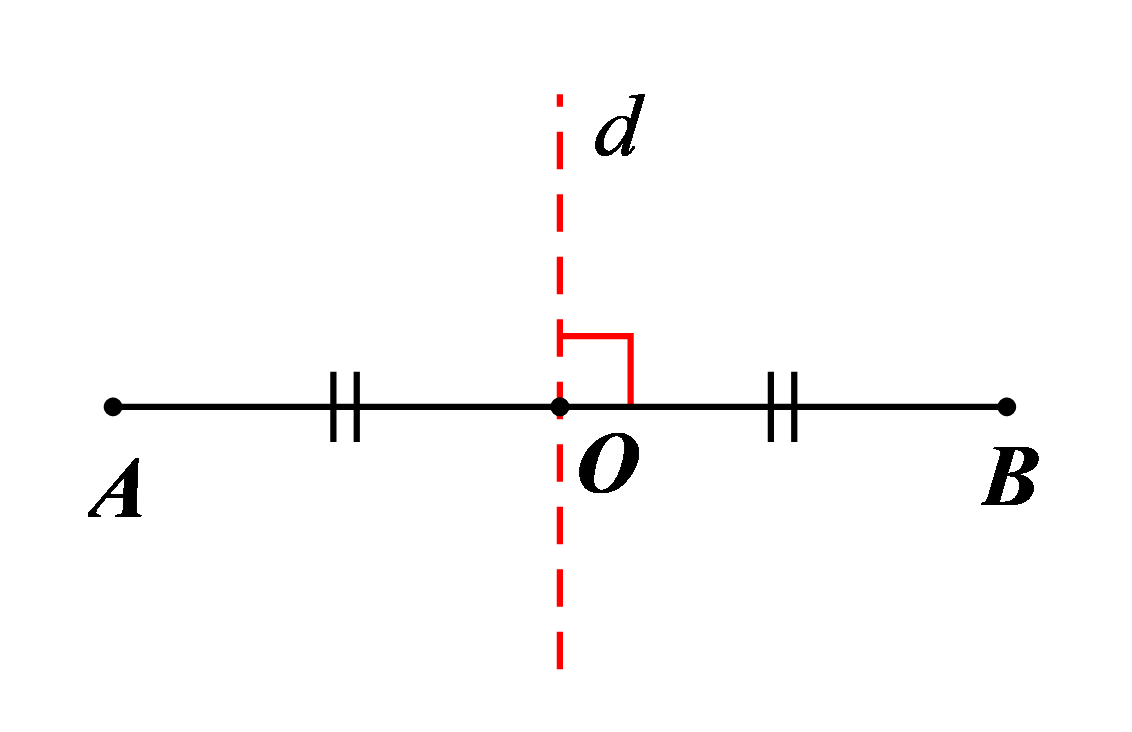
⦁ Đoạn thẳng \(AB\) là hình có trục đối xứng là đường thẳng \[d\] đi qua trung điểm \(O\) của đoạn thẳng \(AB\) và vuông góc với \(AB\) (hình vẽ). Đoạn thẳng \[AB\] là hình có tâm đối xứng và tâm đối xứng là trung điểm \[O\] của \(AB.\) |
|
|
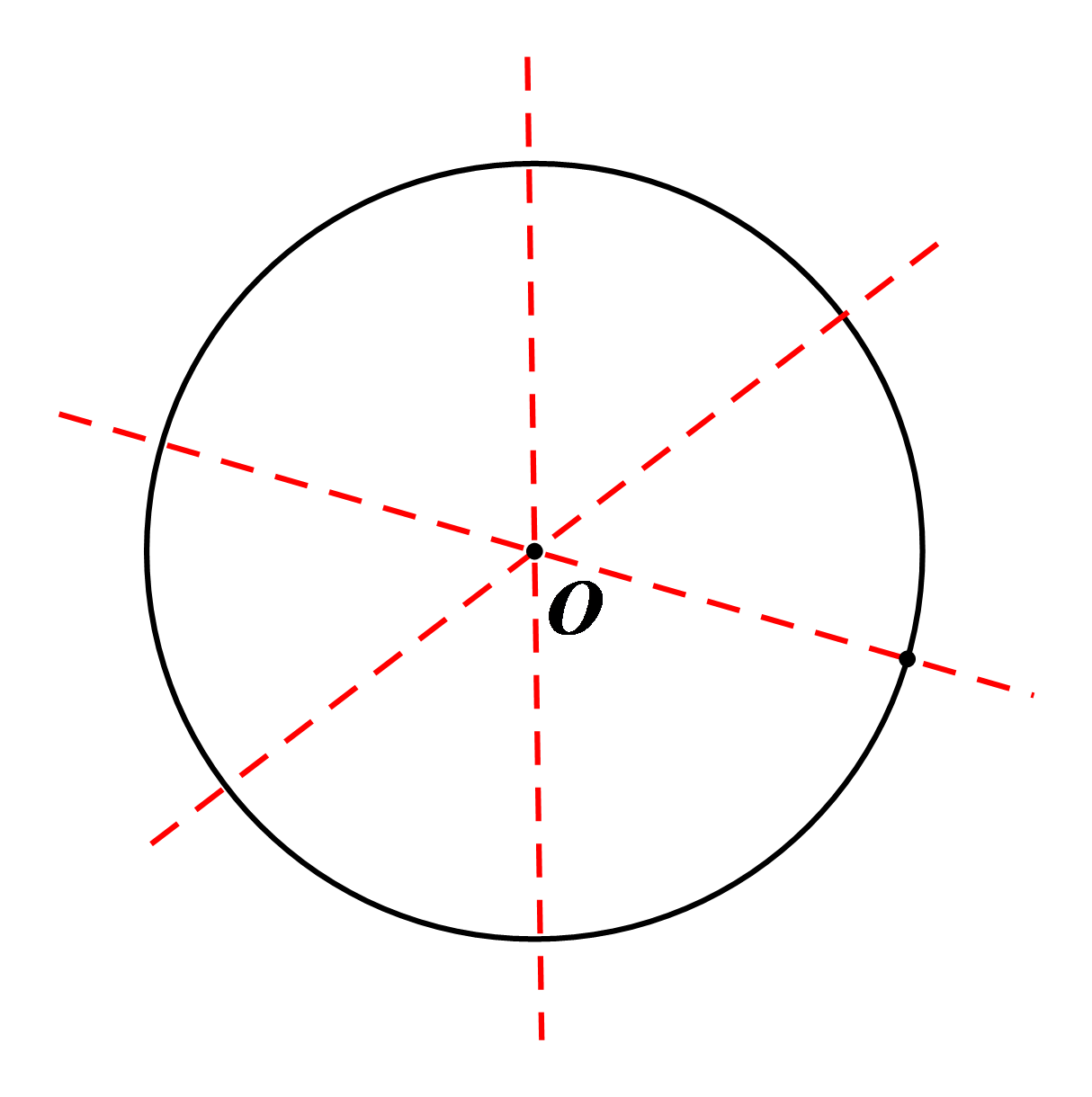
⦁ Hình tròn tâm \[O\] có vô số trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm \[O\] của nó. Hình tròn tâm \[O\] có tâm đối xứng chính là tâm \[O.\] |
 |
|
⦁ Hình thoi \[ABCD\] có 2 trục đối xứng là hai đường chéo \(AC\) và \[BD.\] Hình thoi \[ABCD\] có tâm đối xứng là giao điểm \[O\] của hai đường chéo \(AC\) và \[BD.\] |
|
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
1) a) \(\frac{3}{4} \cdot 26\frac{2}{9} - 38\frac{2}{9} \cdot \frac{3}{4}\) \( = \frac{3}{4} \cdot \left( {26\frac{2}{9} - 38\frac{2}{9}} \right)\) \( = \frac{3}{4} \cdot \left( {26 + \frac{2}{9} - 38 - \frac{2}{9}} \right)\) \( = \frac{3}{4} \cdot \left( { - 12} \right) = - 9.\) |
b) \(0,25 \cdot \frac{7}{{15}} - 25\% \cdot \frac{{ - 8}}{{15}} + 2,75\) \( = 0,25 \cdot \frac{7}{{15}} - 0,25 \cdot \frac{{ - 8}}{{15}} + 2,75\) \( = 0,25 \cdot \left( {\frac{7}{{15}} - \frac{{ - 8}}{{15}}} \right) + 2,75\) \( = 0,25 \cdot \frac{{15}}{{15}} + 2,75\) \( = 0,25 \cdot 1 + 2,75\) \( = 3.\) |
Lời giải
Đáp số: 60.
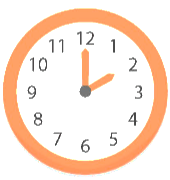
Khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo bằng \(180^\circ .\)
Từ số 12 đến số 6 có 6 khoảng, như vậy, cứ hai số cạnh nhau trên đồng hồ thì có số đo bằng \(\frac{{180^\circ }}{6} = 30^\circ .\)Vậy góc tạo bởi kim phút và kim giờ lúc 2 giờ có số đo là \(2 \cdot 30^\circ = 60^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo