Cho hình vẽ dưới đây. Biết \(AD \bot DC;DC \bot BC\) và độ dài các cạnh \(AB = 13{\rm{ cm, }}AC = 15{\rm{ cm,}}\) \(DC = 12{\rm{ cm}}{\rm{.}}\)
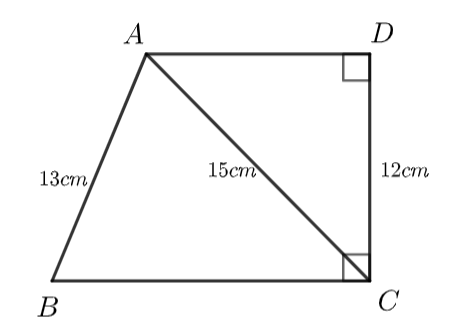
Hỏi độ dài đoạn thẳng \(BC\) bằng bao nhiêu centimet?
Cho hình vẽ dưới đây. Biết \(AD \bot DC;DC \bot BC\) và độ dài các cạnh \(AB = 13{\rm{ cm, }}AC = 15{\rm{ cm,}}\) \(DC = 12{\rm{ cm}}{\rm{.}}\)
Hỏi độ dài đoạn thẳng \(BC\) bằng bao nhiêu centimet?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: \(14\)
Từ \(A\) kẻ đường thẳng \(AE \bot BC\) tại \(E\).
Do đó, \(AECD\) là hình chữ nhật.
Áp dụng định lý Pythagore vào tam giác \(ADC\), ta có: \(A{D^2} + D{C^2} = A{C^2}\) hay \(A{D^2} + {12^2} = {15^2}\)
Suy ra \(AD = \sqrt {{{15}^2} - {{12}^2}} = 9{\rm{ }}\left( {{\rm{cm}}} \right)\).
Ta có: \(DC = AE = 12{\rm{ cm, }}AD = EC = 9{\rm{ cm}}\).
Áp dụng định lý Pythagore vào tam giác \(ABE\), ta có: \(B{E^2} + E{A^2} = A{B^2}\) hay \(B{E^2} + {12^2} = {13^2}\)
Suy ra \(BE = \sqrt {{{13}^2} - {{12}^2}} = 5{\rm{ }}\left( {{\rm{cm}}} \right)\).
Ta có: \(BE + EC = 5 + 9 = 14{\rm{ }}\left( {{\rm{cm}}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đ
a) Với \(m = 0\) thì ta có: \(\left( {d'} \right):y = - 2x + 2.\)
Nhận thấy lúc này hai hệ số góc của hai đường thẳng khác nhau, do đó \(\left( d \right),\left( {d'} \right)\) cắt nhau.
Câu 2
A. \(x \ne 4.\)
B. \(x \ne 2.\)
C. \(x \ne - 2.\)
D. \(x \ne 2;x \ne - 2.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Điều kiện xác định của phân thức \(\frac{{x - 5}}{{{x^2} - 4}}\) là \({x^2} - 4 \ne 0\) hay \({x^2} \ne 4\) nên \(x \ne 2;x \ne - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(0.\)
B. \(\frac{2}{3}.\)
C. \(\frac{{ - 2}}{3}.\)
D. \( - 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(V = S.h.\)
B. \(V = \frac{S}{h}.\)
C. \(V = \frac{1}{2}S.h.\)
D. \(V = \frac{1}{3}S.h.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập