Dựa vào thông tin dưới đây để trả lời các câu từ 72 đến 73
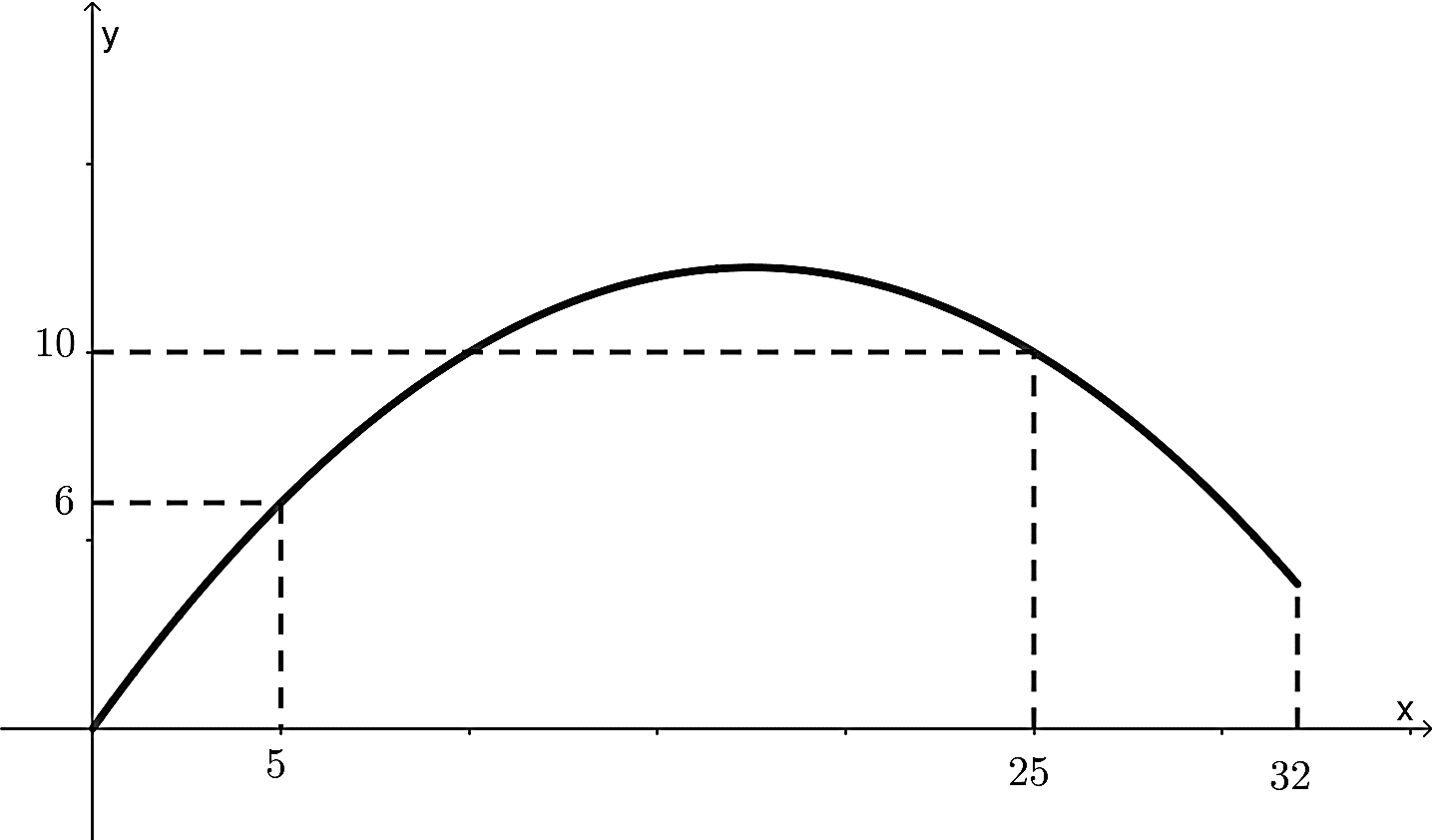
Hai vận động viên \(A\)và \(B\) tham dự một cuộc thi chạy bộ trên một đường thẳng, xuất phát cùng một thời điểm, cùng vạch xuất phát và chạy cùng chiều với vận tốc lần lượt là \({v_A}\) và \({v_B}\). Trong khoảng thời gian \(32\) giây chạy đầu tiên ta có \({v_A} = \frac{1}{{450}}{t^3} - \frac{{47}}{{450}}{t^2} + \frac{{64}}{{45}}t\) (m/s), \({v_B} = a{t^2} + bt\) (m/s) (với \(t \ge 0\) là thời gian tính bằng giây). Hàm số \(y = a{t^2} + bt\) có đồ thị là một phần của parabol như hình vẽ dưới đây.
Khi đó, giá trị của \(a\) là:
Dựa vào thông tin dưới đây để trả lời các câu từ 72 đến 73
Hai vận động viên \(A\)và \(B\) tham dự một cuộc thi chạy bộ trên một đường thẳng, xuất phát cùng một thời điểm, cùng vạch xuất phát và chạy cùng chiều với vận tốc lần lượt là \({v_A}\) và \({v_B}\). Trong khoảng thời gian \(32\) giây chạy đầu tiên ta có \({v_A} = \frac{1}{{450}}{t^3} - \frac{{47}}{{450}}{t^2} + \frac{{64}}{{45}}t\) (m/s), \({v_B} = a{t^2} + bt\) (m/s) (với \(t \ge 0\) là thời gian tính bằng giây). Hàm số \(y = a{t^2} + bt\) có đồ thị là một phần của parabol như hình vẽ dưới đây.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì đồ thị hàm số \(y = a{t^2} + bt\) đi qua các điểm \(A\left( {5;6} \right)\) và \(B\left( {25;10} \right)\).
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{25a + 5b = 6\,\,\,\,\,\,\,}\\{625a + 25b = 10}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{1}{{25}}}\\{b = \frac{7}{5}}\end{array}} \right.\).
Suy ra hàm số vận tốc của vận động viên \(B\) là \({v_B} = - \frac{1}{{25}}{t^2} + \frac{7}{5}t\). Vậy \(a = - \frac{1}{{25}}\). Chọn D.
Câu hỏi cùng đoạn
Câu 2:
Sau \(30\) giây tính từ khi bắt đầu xuất, hai vận động viên cách nhau một khoảng bằng
Lời giải của GV VietJack
Quãng đường vận động viên \(A\) đi được sau \(30\) giây là:
\({s_A} = \int\limits_0^{30} {{v_A}dt} = \int\limits_0^{30} {\left( {\frac{1}{{450}}{t^3} - \frac{{47}}{{450}}{t^2} + \frac{{64}}{{45}}t} \right){\rm{d}}t = 150} \) (m).
Quãng đường vận động viên \(B\) đi được sau \(30\) giây là:
\({s_B} = \int\limits_0^{30} {{v_B}dt} = \int\limits_0^{30} {\left( { - \frac{1}{{25}}{t^2} + \frac{7}{5}t} \right){\rm{d}}t = 270} \) (m).
Khoảng cách sau \(30\) giây tính từ khi bắt đầu xuất của hai vận động viên là:
\({\Delta _S} = {s_A} - {s_B} = \left| {150 - 270} \right| = 120\) (m). Chọn A.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn A
Dung lượng của pin là: q = 3349mAh = 3,349Ah
Thời gian để sạc đầy pin là: \(t = \frac{q}{I} = \frac{{3,349}}{{2,5}} = 1,3396(h) = 1h20\;{\rm{min}}\)
Lời giải
Nếu trong vườn ươm nói trên, cây vú sữa thấp nhất có chiều cao \(71\,cm\) và cây vú sữa cao nhất có chiều cao \(117\,cm\) thì khoảng biến thiên của mẫu số liệu gốc là: \(117 - 71 = 46\) (cm).
Từ biểu đồ, ta có bảng tần số của mẫu số liệu ghép nhóm là:
|
Nhóm |
\(\left[ {70;80} \right)\) |
\(\left[ {80;90} \right)\) |
\(\left[ {90;100} \right)\) |
\(\left[ {100;110} \right)\) |
\(\left[ {110;120} \right)\) |
|
Tần số |
9 |
20 |
33 |
25 |
15 |
Khoảng biến thiên của mẫu số liệu ghép nhóm đã cho là: \(120 - 70 = 50\) (cm).
Do đó khoảng biến thiên của mẫu số liệu ghép nhóm đã cho lớn hơn khoảng biến thiên của mẫu số liệu gốc là \(50 - 46 = 4\) (cm). Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo