PHẦN III. Câu trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 3
Một mô hình áp kế khí như hình vẽ gồm một bình cầu thủy tinh có thể tích 270 cm3 gắn với một ống nhỏ AB nằm ngang có tiết diện 0,1 cm2. Trong ống có một giọt thủy ngân. Ở 0 °C giọt thủy ngân cách A 30 cm. Tính khoảng di chuyển của giọt thủy ngân khi hơ nóng bình cầu đến 10 °C. Coi thể tích bình là không đổi.
PHẦN III. Câu trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 3
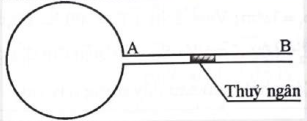
Một mô hình áp kế khí như hình vẽ gồm một bình cầu thủy tinh có thể tích 270 cm3 gắn với một ống nhỏ AB nằm ngang có tiết diện 0,1 cm2. Trong ống có một giọt thủy ngân. Ở 0 °C giọt thủy ngân cách A 30 cm. Tính khoảng di chuyển của giọt thủy ngân khi hơ nóng bình cầu đến 10 °C. Coi thể tích bình là không đổi.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trạng thái thứ nhất khi chất khí ở 0 °C:\(\left\{ {\begin{array}{*{20}{l}}{{{\rm{T}}_1} = 273\;{\rm{K}}}\\{\;{{\rm{V}}_1} = {{\rm{V}}_0} + {\rm{S}}{\ell _1} = 270 + 0,1 \cdot 30 = 273\;{\rm{c}}{{\rm{m}}^3}}\end{array}} \right.{\rm{ }}\)
Trạng thái thứ hai khi chất khí ở 10 °C:\(\left\{ {\begin{array}{*{20}{l}}{{{\rm{T}}_2} = 10 + 273 = 283\;{\rm{K}}}\\{\;{{\rm{V}}_2} = {{\rm{V}}_1} + {\rm{S}}{\ell _2}}\end{array}} \right.\)
Áp dụng định luật Charles cho hai trạng thái có cùng áp suất:
\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow {V_2} = {V_1}\frac{{{T_2}}}{{{T_1}}} = 273 \cdot \frac{{283}}{{273}} = 283\;{\rm{c}}{{\rm{m}}^3} \Rightarrow {\ell _2} = \frac{{{V_2} - {V_1}}}{S} = \frac{{283 - 273}}{{0,1}} = 100\;{\rm{cm}}\)
Khoảng di chuyển của giọt thuỷ ngân là 100 – 30 = 70 cm.
Đáp án: 70 cm.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\[\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow \frac{4}{{7 + 273}} = \frac{{\frac{{12}}{{1,2}}}}{{{T_2}}} \Rightarrow {T_2} = 700K \Rightarrow {t_2} = 427^\circ C\]. Chọn C.
Lời giải
Định luật Charles cho biết thể tích và nhiệt độ tỉ lệ thuận với nhau. Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo