Cho tam giác đều có cạnh bằng 2 cm.
a) Tam giác đều có ba cạnh bằng 2 cm.
b) Tam giác đều có ba góc ở các đỉnh của tam giác bằng nhau.
c) Ghép 2 tam giác đều như trên sao cho một cạnh của tam giác này chồng lên một cạnh của tam giác kia thì ta được một hình vuông.
d) Độ dài đường chéo nhỏ của hình nhận được ở ý c) là 2 cm.
Cho tam giác đều có cạnh bằng 2 cm.
a) Tam giác đều có ba cạnh bằng 2 cm.
b) Tam giác đều có ba góc ở các đỉnh của tam giác bằng nhau.
c) Ghép 2 tam giác đều như trên sao cho một cạnh của tam giác này chồng lên một cạnh của tam giác kia thì ta được một hình vuông.
d) Độ dài đường chéo nhỏ của hình nhận được ở ý c) là 2 cm.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều cấu trúc mới có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: a) Đúng. b) Đúng. c) Sai. d) Đúng.
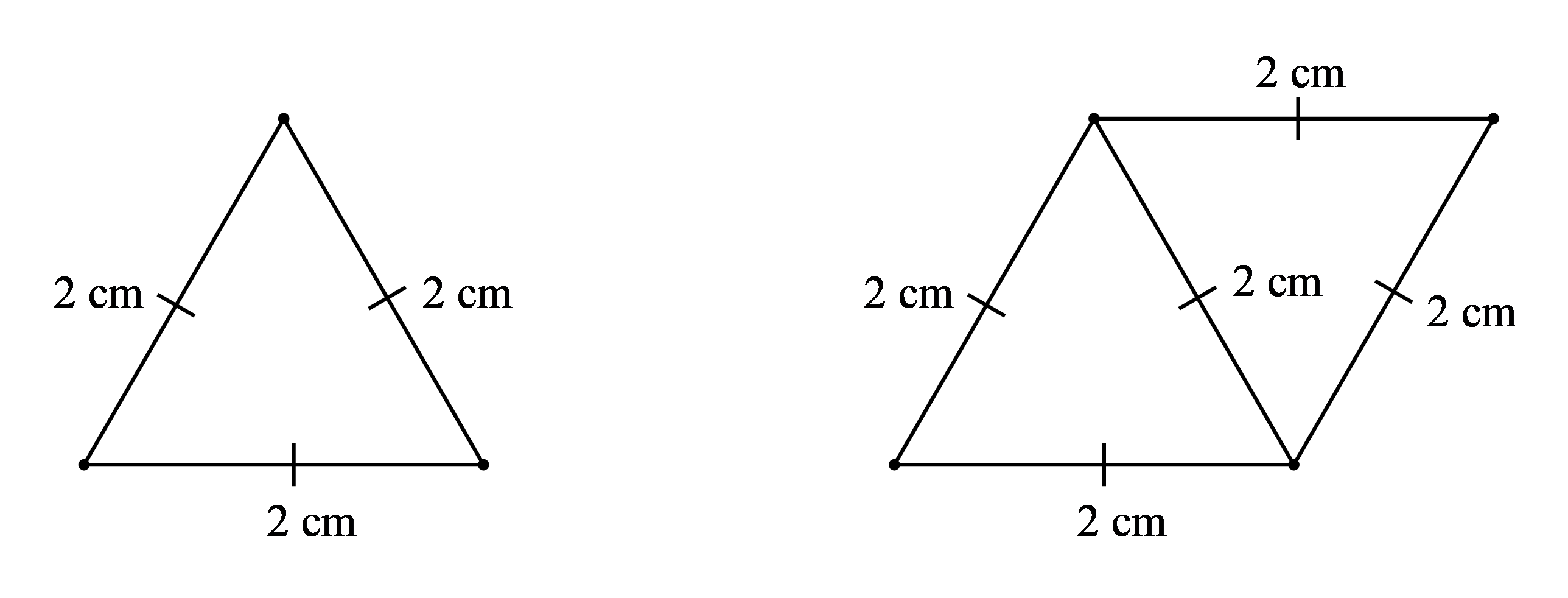
⦁ Tam giác đều có ba cạnh bằng 2 cm. Do đó ý a) là khẳng định đúng.
⦁ Tam giác đều có ba góc ở các đỉnh của tam giác bằng nhau. Do đó ý b) là khẳng định đúng.
⦁ Ghép 2 tam giác đều như trên sao cho một cạnh của tam giác này chồng lên một cạnh của tam giác kia thì ta được một hình thoi (hình vẽ). Do đó ý c) là khẳng định sai.
⦁ Độ dài đường chéo nhỏ của hình nhận được ở ý c) là 2 cm (hình vẽ).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Ô thứ nhất bỏ vào 1 hạt.
Ô thứ hai bỏ vào \(2 = {2^1}\) hạt.
Ô thứ ba bỏ vào \(4 = {2^2}\) hạt.
Ô thứ tư bỏ vào \(8 = {2^3}\) hạt và cứ như vậy, ở ô tiếp theo xếp số hạt gạo gấp đôi ô trước đó nên ô thứ 64 bỏ vào \({2^{63}}\) hạt.
Khi đó, tổng số hạt gạo được Minh xếp lên bàn cờ vua là:
\(S = 1 + {2^1} + {2^2} + {2^3} + ... + {2^{63}}\).
⦁ Ta có: \(2S = {2^1} + {2^2} + {2^3} + {2^4} + ... + {2^{64}}\).
Suy ra \(2S - S = \left( {{2^1} + {2^2} + {2^3} + {2^4} + ... + {2^{64}}} \right) - \left( {1 + {2^1} + {2^2} + {2^3} + ... + {2^{63}}} \right)\)
Do đó, \(S = {2^{64}} - 1.\)
Vậy tổng số hạt gạo được Minh xếp lên bàn cờ vua là: \({2^{64}} - 1\) hạt.
⦁ Ta có: \(S = \left( {1 + {2^1} + {2^2} + {2^3}} \right) + \left( {{2^4} + {2^5} + {2^6} + {2^7}} \right) + ... + \left( {{2^{60}} + {2^{61}} + {2^{62}} + {2^{63}}} \right)\) (gồm có 16 nhóm)
\[S = \left( {1 + {2^1} + {2^2} + {2^3}} \right) + {2^4} \cdot \left( {1 + {2^1} + {2^2} + {2^3}} \right) + ... + {2^{60}} \cdot \left( {1 + {2^1} + {2^2} + {2^3}} \right)\]
\[S = \left( {1 + {2^1} + {2^2} + {2^3}} \right) \cdot \left( {1 + {2^4} + ... + {2^{60}}} \right)\]
\[S = \left( {1 + 2 + 4 + 8} \right) \cdot \left( {1 + {2^4} + ... + {2^{60}}} \right)\]
\[S = 15 \cdot \left( {1 + {2^4} + ... + {2^{60}}} \right)\,\,\, \vdots \,\,\,15.\]
Vậy tổng số hạt gạo được Minh xếp lên bàn cờ vua là một số chia hết cho 15.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
1) a) \(\left[ {\left( {{5^2} \cdot {2^3} - {7^2} \cdot 2} \right):2} \right] \cdot 6 - {3^2} \cdot 17\) \( = \left[ {\left( {{5^2} \cdot {2^2} - {7^2}} \right) \cdot 2:2} \right] \cdot 6 - {3^2} \cdot 17\) \( = \left[ {\left( {25 \cdot 4 - 49} \right) \cdot 1} \right] \cdot 6 - {3^2} \cdot 17\) \( = \left( {100 - 49} \right) \cdot 6 - 3 \cdot 3 \cdot 17\) \( = 51 \cdot 6 - 3 \cdot 51\) \( = 51 \cdot \left( {6 - 3} \right)\) \( = 51 \cdot 3 = 153.\) |
b) \(57 \cdot 34 + 100 \cdot 43 + 57 \cdot 66\) \( = \left( {57 \cdot 34 + 57 \cdot 66} \right) + 100 \cdot 43\) \( = 57 \cdot \left( {34 + 66} \right) + 100 \cdot 43\) \( = 57 \cdot 100 + 100 \cdot 43\) \( = 100 \cdot \left( {57 + 43} \right)\) \( = 100 \cdot 100\) \( = 10\,\,000.\) |
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập