(1,5 điểm) Tìm \(x\), biết:

a) \(5x - {2^3} = {3^3}.\)

b) \(51 - 3\left( {x + 2} \right) = 60.\)

c) \(\left[ {{{\left( {x + 3} \right)}^2} - 8} \right] \cdot 2 = - 14.\)

(0,5 điểm) Một con robot xuất phát từ A đi thẳng đến B. Nó được lập trình cứ tiến 6 bước thì lùi lại 2 bước và để đến được B thì con robot đã thực hiện tổng cộng 126 bước. Hỏi khoảng cách từ A đến B dài bao nhiêu mét, biết mỗi bước đi của robot dài \(5{\rm{\;dm}}.\)

(2,0 điểm) Một khu đất hình thang cân được người ta chia làm hai phần, một phần có dạng hình chữ nhật dùng để làm nhà và một phần còn lại dùng để trồng cỏ bao quanh ngôi nhà với các kích thước như hình vẽ.

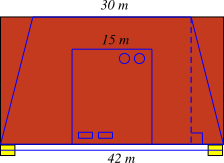
a) Viết công thức tính diện tích hình thang khi biết độ dài hai cạnh đáy \(a,\,\,b\) và chiều cao \(h.\)

b) Tính diện tích khu đất dùng để làm nhà.

c) Nếu mỗi túi hạt giống cỏ gieo vừa đủ trên \(30\,\,{{\rm{m}}^2}\) đất thì cần phải mua bao nhiêu túi hạt giống để gieo hết bãi cỏ? Biết rằng cửa hàng không bán lẻ túi hạt.

(1,5 điểm) Biểu đồ ở hình bên dưới thống kê số lượng ti vi bán được của một cửa hàng điện máy trong bốn tháng cuối năm 2022.

a) Lập bảng thống kê số ti vi cửa hàng bán được trong 4 tháng cuối năm 2022.

b) Tháng nào cửa hàng bán được nhiều ti vi nhất và nhiều hơn tháng bán được ít nhất là bao nhiêu chiếc?

c) Giải bóng đá World Cup 2022 diễn ra vào tháng 11 và tháng 12. Sự kiện đó có liên quan đến việc mua bán ti vi trong thời gian đó hay không?

(2,0 điểm) Thực hiện phép tính (tính hợp lí nếu có thể):

a) \({2^3} \cdot {2^2} + {4^4}:{4^4} - {2^0}.\)

b) \(\left( { - 4} \right) \cdot 8 \cdot \left( { - 125} \right) \cdot \left( { - 3} \right).\)

c) \(27 \cdot 121 - 87 \cdot 27 + 73 \cdot 34.\)

d) \(2\,\,353 - \left( {473 + 2\,\,153} \right) + \left( { - 55 + 373} \right).\)

(2,5 điểm)

1. Một người kinh doanh quán phở ở hà Nội ghi số tiền lợi nhuận của cửa hàng trong 5 ngày như sau:

Em hãy cho biết:

a) Trong 5 ngày trên, có mấy ngày cửa hàng kinh doanh lỗ?

b) Sau 5 ngày trên, cửa hàng kinh doanh lãi hay lỗ bao nhiêu tiền?

2. Số học sinh khối 6 của một trường THCS khi xếp hàng 15, 20, 25 đều thiếu 1 người. Tính số học sinh khối 6 của trường đó biết rằng số học sinh đó chưa đến 400.