Cho đoạn thẳng \(AB = 9{\rm{ cm}}\). Trên tia \(AB\) lấy điểm \(M\) sao cho \(AM = 3{\rm{ cm}}\). Gọi \(I\) là trung điểm của \(MB.\)
a) Tính độ dài \(MI.\)
b) Chứng tỏ rằng \(M\) là trung điểm của đoạn thẳng \(AI.\)
Cho đoạn thẳng \(AB = 9{\rm{ cm}}\). Trên tia \(AB\) lấy điểm \(M\) sao cho \(AM = 3{\rm{ cm}}\). Gọi \(I\) là trung điểm của \(MB.\)
a) Tính độ dài \(MI.\)
b) Chứng tỏ rằng \(M\) là trung điểm của đoạn thẳng \(AI.\)
Quảng cáo
Trả lời:
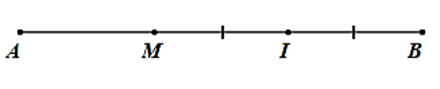
a) Trên \(AB\), có \(AM < AB{\rm{ }}\left( {3{\rm{ cm}} < 9{\rm{ cm}}} \right)\).
Nên \(M\) nằm giữa hai điểm \(A,B\).
Ta có: \(AM + MB = AB\) nên \(MB = AB - AM = 9 - 3 = 6{\rm{ cm}}{\rm{.}}\)
Mà \(I\) là trung điểm của \(MB\) nên \(MI = IB = \frac{1}{2}MB = 3{\rm{ cm}}{\rm{.}}\)
Vậy \(MI = 3{\rm{ cm}}{\rm{.}}\)
b) Vì \(M\) nằm giữa hai điểm \(A,B\) và \(I\) là trung điểm của \(MB\) nên \(M\) nằm giữa hai điểm \(A,I.\)
Mà \(MI = AM = 3{\rm{ cm}}{\rm{.}}\)
Do đó, \(M\) là trung điểm của đoạn thẳng \(AI.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
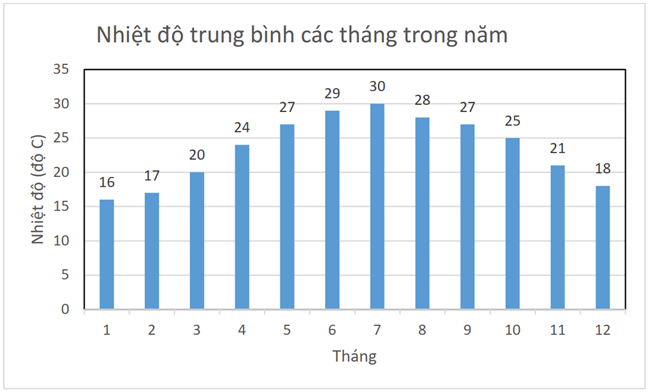
A. Tháng 5.
Lời giải
Đáp án đúng là: C
Tháng có nhiệt độ trung bình cao nhất là tháng 7 với nhiệt độ trung bình là \(30^\circ C\).
Lời giải
Đáp án đúng là: a) Đ b) Đ c) S d) S
a) Đối tượng thống kê: Ngày thứ nhất, ngày thứ hai, ngày thứ ba, ngày thứ tư.
b) Tiêu chí thống kê: Số bánh mì bán được trong bốn ngày gần đây.
c) Số bánh mì bán được ở ngày thứ nhất là: \(4.10 + 5 = 45\) (chiếc)
Số bánh mì bán được ở ngày thứ hai là: \(3.10 + 5 = 35\) (chiếc)
Số bánh mì bán được ở ngày thứ ba là: \(6.10 = 60\) (chiếc)
Số bánh mì bán được ở ngày thứ tư là: \(3.10 = 30\) (chiếc)
Tổng số bánh mì cửa hàng bán được sau bốn ngày là: \(45 + 35 + 60 + 30 = 170\) (chiếc)
d) Doanh thu cửa hàng bán được ở ngày thứ ba là: \(60.5{\rm{ }}000 = 300{\rm{ 000}}\) (đồng)
Doanh thu cửa hàng bán được ở ngày thứ hai là: \(35.5000 = 175{\rm{ }}000\) (đồng)
Ta có: \(300{\rm{ }}000:175{\rm{ }}000 = \frac{{12}}{7} < \frac{{14}}{7} = 2\).
Vậy doanh thu của cửa hàng bán được ở ngày thứ ba gấp \(2\) lần doanh thu của ngày thứ hai là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. chia đoạn thẳng thành hai phần bằng nhau.
B. chia đoạn thẳng thành ba phần bằng nhau.
C. chia đoạn thẳng thành hai phần không bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.