Trong các khẳng định sau, khẳng định nào sai?
A. Ước chung của hai số tự nhiên \(a\) và \(b\) là ước của ước chung lớn nhất của chúng.
B. Bội chung của hai số tự nhiên \(a\) và \(b\) là bội của bội chung nhỏ nhất của chúng.
C. ƯCLN\(\left( {a,\,\,b} \right)\) là ước của BCNN\(\left( {a,\,\,b} \right).\)
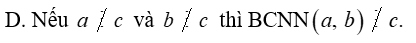
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 1 Toán 6 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: 7.
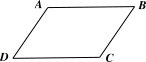
Vì \(ABCD\) là hình bình hành nên chu vi của hình bình hành này là: \(2 \cdot \left( {AB + BC} \right) = 2 \cdot \left( {8 + BC} \right).\)
Do đó, ta có: \(2 \cdot \left( {8 + BC} \right) = 30\)
Suy ra \(8 + BC = 15\) nên \(BC = 7\) (cm).
Lời giải
Hướng dẫn giải
Gọi \(x\) (học sinh) là số học sinh khối 6 nhập học tại trường THCS đó \(\left( {x \in \mathbb{N}*,\,\,500 < x < 600} \right).\)
Nếu xếp hàng 18, hàng 27, hàng 30 thì đều vừa đủ nên ta có \(x\,\, \vdots \,\,18,\) \(x\,\, \vdots \,\,27,\) \(x\,\, \vdots \,\,30.\)
Do đó \[x \in \]BC\(\left( {18,\,\,27,\,\,30} \right).\)
Ta có: \(18 = 2 \cdot {3^2};\,\,\,\,\,27 = {3^3};\,\,\,\,\,30 = 2 \cdot 3 \cdot 5.\)
Suy ra BCNN\(\left( {18,\,\,27,\,\,30} \right) = 2 \cdot {3^3} \cdot 5 = 270.\)
Nên BC\(\left( {18,\,\,27,\,\,30} \right) = \)B\[\left( {270} \right) = \left\{ {0;\,\,270;\,\,540;\,\,810;\,\,...} \right\}.\]
Hay \(x \in \left\{ {0;\,\,270;\,\,540;\,\,810;\,\,...} \right\}.\)
Mà \(500 < x < 600\) nên \[x = 540\] (thỏa mãn).
Vậy trường THCS đó có 540 học sinh khối lớp 6 đến nhập học.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 2 cm.
B. 4 cm.
C. 3 cm.
D. 6 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.