Cho lục giác đều \[ABCDEF\] có tâm \[O\] như hình vẽ bên dưới.
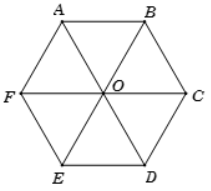
a) \[OB,{\rm{ }}OC\] là các đường chéo chính của lục giác đều.
b) \[AB = BC = AF.\]
c) \[ABCF\] là một hình thang cân.
d) Hình vẽ đã cho có tất cả 4 hình thang cân.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: a) Sai.b) Đúng.c) Đúng.d) Sai.
⦁ Hình lục giác đều \[ABCDEF\] có ba đường chéo chính là \[AD,{\rm{ }}BE,{\rm{ }}CF.\] Do đó ý a) sai.
⦁ Vì \[ABCDEF\] là lục giác đều nên \[AB = BC = AF\] (hình lục giác đều có sáu cạnh bằng nhau). Do đó ý b) đúng.
⦁ Vì \[ABCDEF\] là lục giác đều nên \[ABCF\] là hình thang cân. Do đó ý c) đúng.
⦁ Hình vẽ đã cho có tất cả 6 hình thang cân là \[ABCF,{\rm{ }}CDEF,{\rm{ }}ABCD,{\rm{ }}DEFA,{\rm{ }}BCDE,{\rm{ }}EFAB.\] Do đó ý d) sai.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
|
a) \(\left( {179 + 32 - 25} \right) - \left( {179 - 75 + 32} \right)\) \( = 179 + 32 - 25 - 179 + 75 - 32\) \( = \left( {179 - 179} \right) + \left( {32 - 32} \right) + \left( { - 25 + 75} \right)\) \( = 0 + 0 + 50\) \( = 50.\) |
b) \( - 79 \cdot 51 + 79 \cdot \left( { - 48} \right) - 79\) \( = 79 \cdot \left( { - 51} \right) + 79 \cdot \left( { - 48} \right) - 79\) \( = 79 \cdot \left[ {\left( { - 51} \right) + \left( { - 48} \right) - 1} \right]\) \( = 79 \cdot \left[ { - 100} \right]\) \( = - 7\,\,900.\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp số: 12.
\(4\left( {x + 1} \right) - 5\left( { - 3 + x} \right) = 7\)
\(4x + 4 + 15 - 5x = 7\)
\( - x = - 12\)
\(x = 12.\)
Vậy \(x = 12.\)
Câu 3
A. 10.
B. 15.
C. 16.
D. 17.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Gà chín cựa.
B. Ngựa chín hồng mao.
C. Bánh dày.
D. Bánh chưng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Phần tử 2 vừa thuộc tập hợp \[A\] vừa thuộc tập hợp \[B.\]
B. Phần tử 6 chỉ thuộc tập hợp \[A.\]
C. Phần tử 5 chỉ thuộc tập hợp \[B.\]
D. Phần tử 8 vừa thuộc tập hợp \[A\] vừa thuộc tập hợp \[B.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập