(0,5 điểm) Cho \(a + b + c = 0\) và \({a^2} + {b^2} + {c^2} = 1.\) Tính giá trị của biểu thức \(A = {a^4} + {b^4} + {c^4}.\)
Quảng cáo
Trả lời:
Hướng dẫn giải
Ta có \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)\).
Suy ra \({0^2} = 1 + 2\left( {ab + bc + ca} \right)\).
Do đó \(ab + bc + ca = - \frac{1}{2}.\)
Khi đó \(A = {a^4} + {b^4} + {c^4} = {\left( {{a^2} + {b^2} + {c^2}} \right)^2} - 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right)\)
\( = {\left( {{a^2} + {b^2} + {c^2}} \right)^2} - 2\left[ {{{\left( {ab} \right)}^2} + {{\left( {bc} \right)}^2} + {{\left( {ca} \right)}^2}} \right]\)
\( = {\left( {{a^2} + {b^2} + {c^2}} \right)^2} - 2\left[ {{{\left( {ab + bc + ca} \right)}^2} - 2abc\left( {a + b + c} \right)} \right]\)
\( = {1^2} - 2\left[ {{{\left( { - \frac{1}{2}} \right)}^2} - 2abc \cdot 0} \right]\)
\( = 1 - 2 \cdot \frac{1}{4} = \frac{1}{2}.\)
Vậy \(A = \frac{1}{2}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án:
a) Sai.
b) Đúng.
c) Sai.
d) Sai.
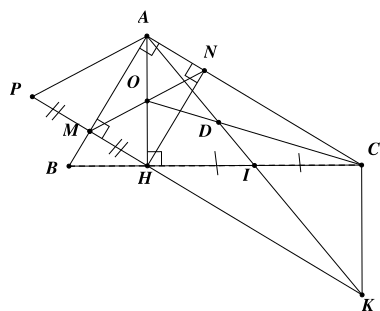
⦁ Tứ giác \(AHKC\) có hai đường chéo cắt nhau tại trung điểm \(I\) của mỗi đường nên là hình bình hành nên \(\widehat {HKC} = \widehat {HAC}\). Do đó ý a) sai.
⦁ Xét tứ giác \(AMHN\) có \(\widehat {AMH} = \widehat {MAN} = \widehat {ANH} = {\rm{90^\circ }}\)
Do đó tứ giác \[AMHN\] là hình chữ nhật. Do đó ý b) đúng.
⦁ Khi đó \(OA = ON = OM = OH\) nên \(\Delta OMH\) cân tại \(O\,.\)
Suy ra \(\widehat {OMH} = \widehat {OHM}\) mà \(\widehat {HKC} = \widehat {OHM}\) (so le trong) nên \(\widehat {HKC} = \widehat {OMH}\).
Mặt khác \(\widehat {HKC} = \widehat {HAC}\) (chứng minh ý a) nên \(\widehat {OMH} = \widehat {HKC}\).
Hình thang \(MNCK\) có hai góc kề một đáy bằng nhau nên là hình thang cân. Do đó ý c) sai.
⦁ Vì \(\Delta AHC\) có hai đường trung tuyến \(AI,\,\,CO\) cắt nhau tại \(D\) nên \(D\) là trọng tâm nên
\(AD = \frac{2}{3}AI\) mà \(AI = \frac{1}{2}AK.\)
Thay vào ta được \(AD = \frac{2}{3} \cdot \frac{1}{2}AK = \frac{1}{3}AK\) nên \(AK = 3AD\). Do đó ý d) sai.
Lời giải
Hướng dẫn giải:
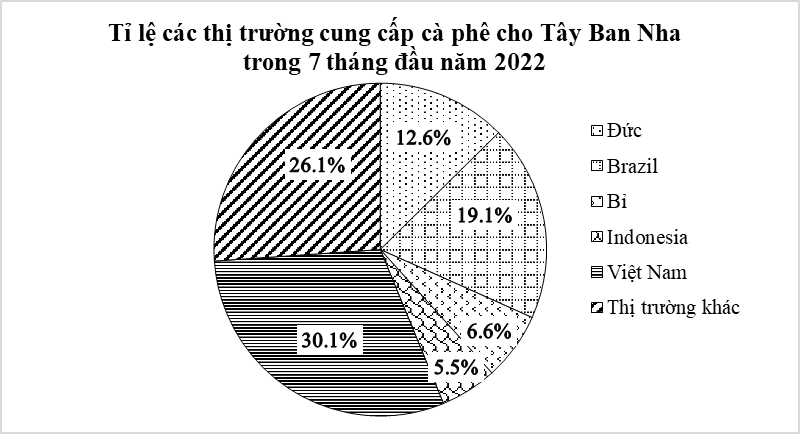
a) Trong 7 tháng đầu năm 2022 thị trường cung cấp cà phê cho Tây Ban Nha nhiều nhất là thị trường Việt Nam \((30,1\% )\); ít nhất là thị trường Indonesia \((5,5\% )\).
b) Các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022:
Lượng cà phê thị trường Đức cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,12,6\% = 28\,\,092,456\] (tấn)
Lượng cà phê thị trường Brazil cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,19,1\% = 42\,\,584,596\] (tấn)
Lượng cà phê thị trường Bỉ cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,6,6\% = 14\,\,715,096\] (tấn)
Lượng cà phê thị trường Indonesia cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,5,5\% = 12\,\,262,58\] (tấn)
Lượng cà phê thị trường Việt Nam cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,30,1\% = 67\,\,109,756\] (tấn)
Lượng cà phê thị trường khác cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,26,1\% = 58\,\,191,516\] (tấn)
Từ đó, ta có bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 như sau:

c) Thị trường Indonesia và Bỉ là hai thị trường cung cấp lượng cà phê ít nhất cho Tây Ban Nha trong 7 tháng đầu năm 2022.
Việt Nam cung cấp cà phê cho Tây Ban Nha nhiều hơn \[24,6\% \] so với thị trường Indonesia (vì \[30,1\% - 5,5\% = 24,6\% \]).
Theo em, bài báo nêu thông tin chính xác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[5{x^3}{y^2}\].
B. \[6{y^4}\].
C. \[60xy\].
D. \[30{x^4}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(87,3\% \).
B. \(9,9\% \).
C. \(13,8\% \).
D. \(87,5\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.