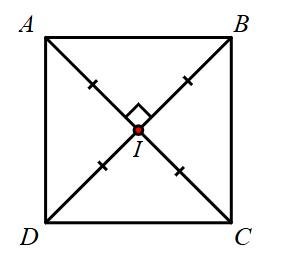
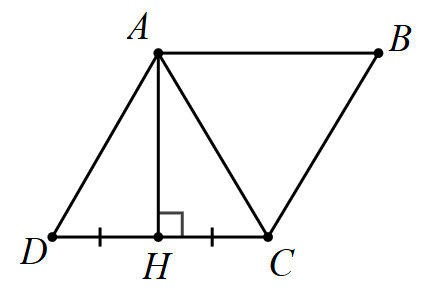
Cho hình vẽ sau.
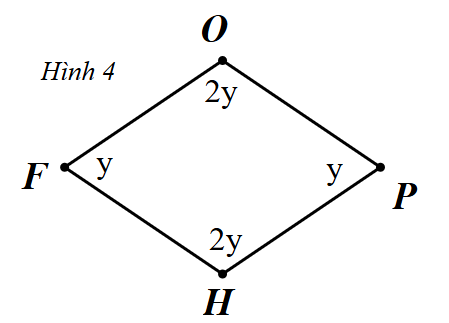
Hãy chọn khẳng định sai.
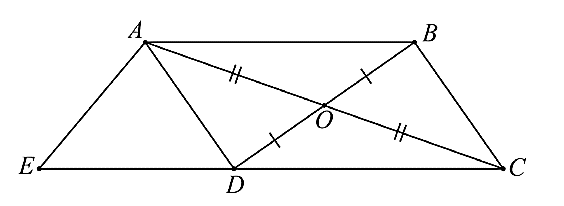
Cho hình vẽ sau.
A. \(ABCD\) là hình bình hành.
B. \(\Delta ABC = \Delta CDA\).
C. \(ABCD\) là hình thang cân.
D. \(BC\parallel AD.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
• Nhận thấy tứ giác \(ABCD\) có hai đường chéo \(AC,BD\) cắt nhau tại giao điểm \(O\) cũng chính là trung điểm mỗi đường. Do đó, \(ABCD\) là hình bình hành.
• Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(AC\) chung (gt)
\(AD = BC\) (\(ABCD\) là hình bình hành)
\(AB = DC\) (\(ABCD\) là hình bình hành).
Do đó, \(\Delta ABC = \Delta CDA\) (c.c.c)
Do đó, chọn đáp án C.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(125^\circ .\)
B. \(65^\circ .\)
C. \(90^\circ .\)
D. \(55^\circ .\)
Lời giải
Đáp án đúng là: A
Vì \(ABCD\) là hình thang cân có hai đáy \(AB\parallel CD\) nên \(\widehat A = \widehat B = 125^\circ \) (hai góc kề một đáy).
Câu 2
A. Có hai đường chéo bằng nhau.
B. Có hai đường chéo vuông góc.
C. Có hai góc kề một đáy bằng nhau.
D. Có một góc vuông.
Lời giải
Đáp án đúng là: D
Để hình thang cân trở thành hình chữ nhật thì cần thêm điều kiện có một góc vuông.
Câu 3
A. Có một góc vuông.
B. Có hai cạnh kề bằng nhau.
C. Có hai đường chéo bằng nhau.
D. Có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(25^\circ .\)
B. \(50^\circ .\)
C. \(90^\circ .\)
D. \(130^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Hình thoi có một góc vuông.
B. Hình chữ nhật có hai đường chéo bằng nhau.
C. Hình bình hành có hai đường chéo bằng nhau.
D. Hình thoi có hai đường chéo bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\widehat B = \widehat D = 80^\circ ,\widehat A = \widehat C = 100^\circ .\)
B. \(\widehat B = \widehat D = 120^\circ ,\widehat A = \widehat C = 60^\circ .\)
C. \(\widehat B = \widehat C = 60^\circ ,\widehat A = \widehat D = 120^\circ .\)
D. \(\widehat B = \widehat D = 60^\circ ,\widehat A = \widehat C = 120^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập