Cho hình vuông \(ABCD.\) Trên cạnh \(AB,BC,CD,DA\) lần lượt lấy các điểm \(E,F,G,H\) sao cho \(AE = BF = CG = DH\).

          a) \(AH = BE = CF = DG.\)

          b) \(\Delta AEH = \Delta BEF\).

          c) \(\widehat {FEH} < 90^\circ \).

          d) \(EFGH\) là hình vuông.

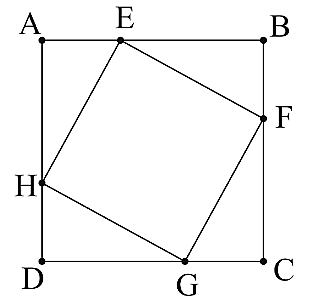
a) Đúng.

Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\).

Mà \(AE = BF = CG = DH\) nên \(AH = BE = CF = DG.\)

b) Sai.

Xét \(\Delta AEH\) và \(\Delta BEF\), có:

\(AE = BF\) (gt)

\(AH = BE\) (cmt)

Do đó, \(\Delta AEH = \Delta BFE\) (2cgv).

c) Sai.

Vì \(\Delta AEH = \Delta BFE\) (cmt) nên \[\widehat {AEH} = \widehat {BFE}\] (hai góc tương ứng).

Trong tam giác \(\Delta BFE\) vuông tại \(B\) có: \[\widehat {FEB} + \widehat {BFE} = 90^\circ \] (phụ nhau).

Mà \[\widehat {AEH} = \widehat {BFE}\] (cmt) nên \[\widehat {AEH} + \widehat {BEF} = 90^\circ \].

Ta có: \[\widehat {AEH} + \widehat {BEF} + \widehat {HEF} = 180^\circ \]

Suy ra \[\widehat {HEF} = 180^\circ - \left( {\widehat {AEH} + \widehat {BEF}} \right) = 180^\circ - 90^\circ = 90^\circ \].

Vậy \(\widehat {FEH} = 90^\circ .\)

d) Đúng.

Vì có \(AB = BC = CD = DA\) và \(AE = BF = CG = DH\) nên

ta chứng minh được \(\Delta AEH = \Delta BFE = \Delta CGF = \Delta DHG\).

Suy ra \(HE = EF = FG = GH\) nên \(EFGH\) là hình thoi.

Mà \(\widehat {FEH} = 90^\circ \) nên \(EFGH\) là hình vuông.