Cho hình vuông \(ABCD.\) Gọi \(M,N,P,Q\) là trung điểm các cạnh \(AB,BC,CD,CA\). Tính tỉ số \(\frac{{{S_{MNPQ}}}}{{{S_{ABCD}}}}\). (Kết quả ghi dưới dạng số thập phân)
Cho hình vuông \(ABCD.\) Gọi \(M,N,P,Q\) là trung điểm các cạnh \(AB,BC,CD,CA\). Tính tỉ số \(\frac{{{S_{MNPQ}}}}{{{S_{ABCD}}}}\). (Kết quả ghi dưới dạng số thập phân)
Câu hỏi trong đề: Trắc nghiệm Bài tập cuối chương 3 lớp 8 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 0,5
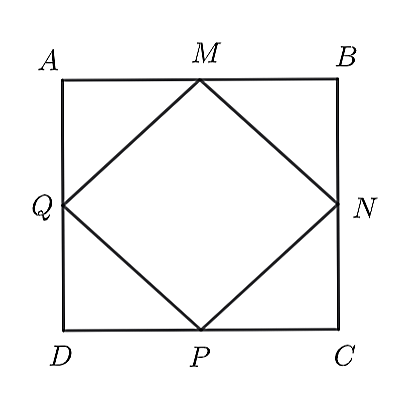
Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\).
Mà \(M,N,P,Q\) là trung điểm các cạnh \(AB,BC,CD,CA\)
nên \(AM = MB = BN = NC = CP = PD = DQ = DA\).
Do đó, ta chứng minh được các tam giác \(AQM,{\rm{ }}NBM,{\rm{ }}NCP,{\rm{ }}QPD\) là các tam giác vuông cân bằng nhau.
Ta có: \({S_{\Delta AQM}} = {S_{\Delta BMN}} = {S_{\Delta NPC}} = {S_{\Delta PDQ}} = \frac{1}{2} \cdot AM \cdot AQ = \frac{1}{2} \cdot \frac{1}{2}AB \cdot \frac{1}{2}AD = \frac{1}{8}AB \cdot AD = \frac{1}{8}{S_{ABCD}}\).
Mà ta có: \({S_{MNPQ}} = {S_{ABCD}} - \left( {{S_{\Delta AMQ}} + {S_{\Delta BMN}} + {S_{\Delta PNC}} + {S_{\Delta QPD}}} \right) = {S_{ABCD}} - 4 \cdot \frac{1}{8}{S_{ABCD}} = \frac{1}{2}{S_{ABCD}}\).
Vậy \(\frac{{{S_{MNPQ}}}}{{{S_{ABCD}}}} = \frac{{\frac{1}{2}{S_{ABCD}}}}{{{S_{ABCD}}}} = \frac{1}{2} = 0,5.\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: A
Vì \(ABCD\) là hình thang cân có hai đáy \(AB\parallel CD\) nên \(\widehat A = \widehat B = 125^\circ \) (hai góc kề một đáy).
Câu 2
Lời giải
Đáp án đúng là: D
Nhận thấy đường cao \(AH\) kẻ từ đỉnh \(A\) đến cạnh \(CD\) chia cạnh đó thành hai đoạn bằng nhau.
Suy ra \(AH\) cũng đường đường trung trực trong \(\Delta ADC\) là tam giác cân tại \(A\).
Suy ra \(AD = AC\) (1)
Lại có \(ABCD\) là hình thoi nên \(AD = DC\) (2).
Từ (1) và (2) suy ra \(\Delta ADC\) đều.
Suy ra \(\widehat {ADC} = \widehat {DCA} = \widehat {DAC} = 60^\circ \).
Vì \(ABCD\) là hình thoi nên \(\widehat D = \widehat B = 60^\circ ,\widehat A = \widehat C = 120^\circ \).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập