Cho hàm số \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}}\) (1), với \(m\) là số thực.
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số có đường tiệm cận xiên là \(y = x - 2\).
c) Khi \(m = 1\) giao điểm của đường tiệm cận xiên và tiệm cận đứng của đồ thị hàm số là \(I\left( {3; - 5} \right)\).
d) Có 2 giá trị \(m\) để góc giữa hai tiệm cận của đồ thị hàm số (1) bằng \(45^\circ \).
Cho hàm số \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}}\) (1), với \(m\) là số thực.
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số có đường tiệm cận xiên là \(y = x - 2\).
c) Khi \(m = 1\) giao điểm của đường tiệm cận xiên và tiệm cận đứng của đồ thị hàm số là \(I\left( {3; - 5} \right)\).
d) Có 2 giá trị \(m\) để góc giữa hai tiệm cận của đồ thị hàm số (1) bằng \(45^\circ \).
Quảng cáo
Trả lời:
Với \(m = 1\), hàm số có dạng \(y = \frac{{{x^2} + x - 2}}{{x + 3}} = x - 2 + \frac{4}{{x + 3}}\).
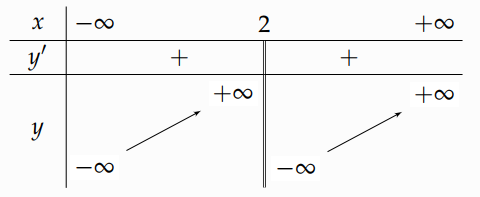
a) Ta có \(y' = 1 - \frac{4}{{{{\left( {x + 3} \right)}^2}}}\); \(y' = 0 \Leftrightarrow 1 - \frac{4}{{{{\left( {x + 3} \right)}^2}}} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\).
Bảng biến thiên
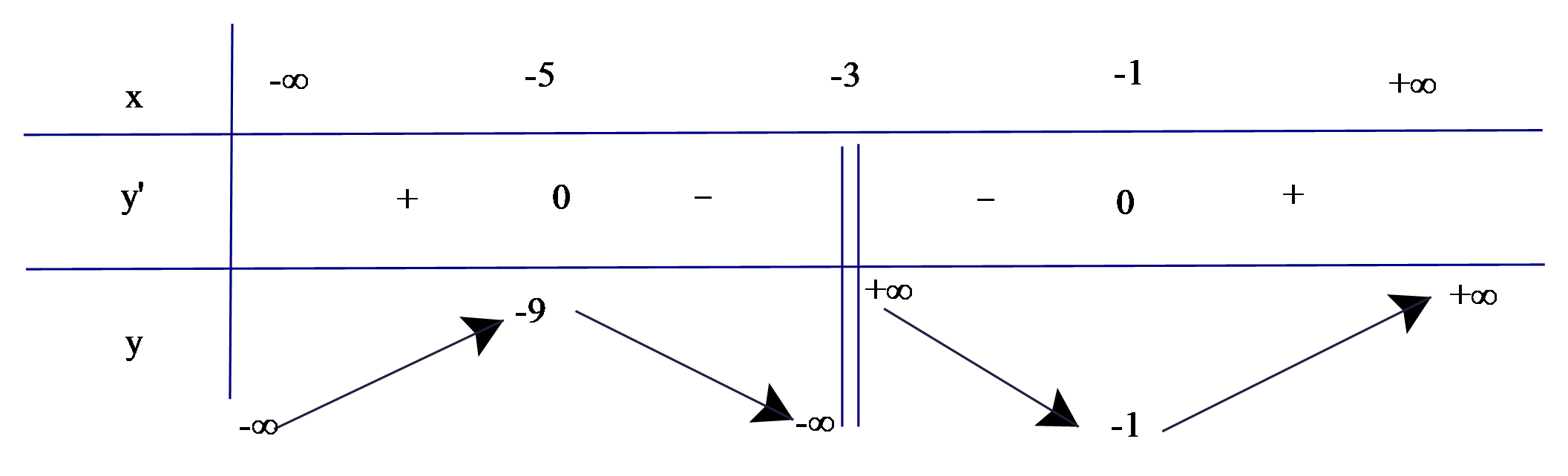
Dựa vào bảng biến thiên, hàm số có 2 điểm cực trị.
b) Có \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 2} \right)} \right] = 0\) nên \(y = x - 2\) là tiệm cận xiên của đồ thị hàm số.
c) \(\mathop {\lim }\limits_{x \to - {3^ + }} \frac{{{x^2} + x - 2}}{{x + 3}} = + \infty \); \(\mathop {\lim }\limits_{x \to - {3^ - }} \frac{{{x^2} + x - 2}}{{x + 3}} = - \infty \) nên \(x = - 3\) là tiệm cận đứng của đồ thị hàm số.
Thay \(x = - 3\) vào \(y = x - 2\) được \(y = 1\).
Do đó giao điểm của tiệm cận đứng và tiệm cận xiên là \(I\left( { - 3;1} \right)\).
d) Ta có: \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}} = mx - 2 + \frac{{6m - 2}}{{x + 3m}}\)
* Nếu \(m = \frac{1}{3}\) đồ thị hàm số không tồn tại hai tiệm cận
* Nếu \(m \ne \frac{1}{3}\), đồ thị hàm số có hai tiệm cận
\({d_1}:x = - 3m \Leftrightarrow x + 3m = 0\) và \({d_2}:y = mx - 2 \Leftrightarrow mx - y - 2 = 0\).
\( \Rightarrow \overrightarrow {{n_1}} (1;0),{\rm{ }}\overrightarrow {{n_2}} (m; - 1)\) lần lượt là vectơ pháp tuyến của \({d_1}\) và \({d_2}\).
Góc giữa \({d_1}\) và \({d_2}\) bằng \(45^\circ \Leftrightarrow \cos 45^\circ = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\)\( \Leftrightarrow \frac{{\left| m \right|}}{{\sqrt {{m^2} + 1} }} = \frac{{\sqrt 2 }}{2} \Leftrightarrow m = \pm 1\).
Đáp án: a) Đúng; b) Đúng; c) Sai; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
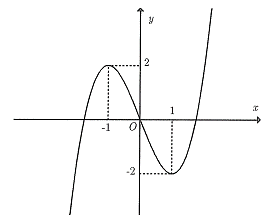
Dựa vào bảng biến thiên ta thấy
Tiệm cận đứng là đường thẳng \(x = 2\).
Đạo hàm \(y' > 0\) với mọi \(x \ne 2\)
+) Xét đáp án A: Có \(y' = \frac{{2x\left( {x - 2} \right) - \left( {{x^2} - 3} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}}\).
+) Xét đáp án B: Có \(y' = \frac{{\left( {2x - 4} \right)\left( {x - 2} \right) - \left( {{x^2} - 4x + 2} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 6}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{{\left( {x - 2} \right)}^2} + 2}}{{{{\left( {x - 2} \right)}^2}}} > 0,\forall x \ne 2\).
+) Xét đáp án C: Có \(y' = \frac{{\left( {2x - 1} \right)\left( {x - 2} \right) - \left( {{x^2} - x} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \)\( = \frac{{{x^2} - 4x + 2}}{{{{\left( {x - 2} \right)}^2}}}\).
+) Xét đáp án D: Có \(y' = \frac{{\left( {2x - 4} \right)\left( {x - 2} \right) - \left( {{x^2} - 4x + 5} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}}\). Chọn B.
Câu 2
Lời giải
Ta có: \(S = {t^3} - 3{t^2} - 9t + 2\)
Khi vận tốc bị triệt tiêu tức \(v = 0 \Leftrightarrow 3{t^2} - 6t - 9 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1 < 0\\t = 3\left( {tm} \right)\end{array} \right.\).
Khi đó gia tốc tại thời điểm vận tốc bị triệt tiêu là \(a = 6.3 - 6 = 12\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.