Một cái bơm chứa 100 cm3 không khí ở nhiệt độ 27 °C và áp suất 105 Pa. Tính áp suất của không khí bị nén xuống còn 20 cm3 và nhiệt độ tăng lên tới 39 °C.
A. \({{\rm{p}}_2} = 5,2 \cdot {10^4}\;{\rm{Pa}}.\)
B. \({{\rm{p}}_2} = {6.10^5}\;{\rm{Pa}}.\)
C. \({{\rm{p}}_2} = 5,2 \cdot {10^5}\;{\rm{Pa}}.\)
D. \({{\rm{p}}_2} = {5.10^5}\;{\rm{Pa}}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow \frac{{{{10}^5}.100}}{{27 + 273}} = \frac{{{p_2}.20}}{{39 + 273}} \Rightarrow {p_2} = {5,2.10^5}Pa\]. Chọn C.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 1 atm; 6 lít.
B. 2 atm; 3 lít.
C. 2 atm; 6 lít.
D. 4 atm; 6 lít.
Lời giải
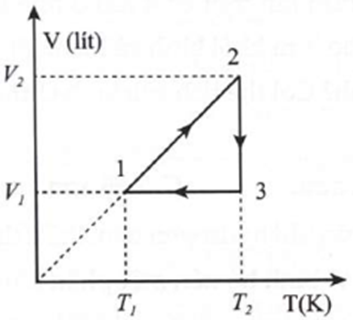
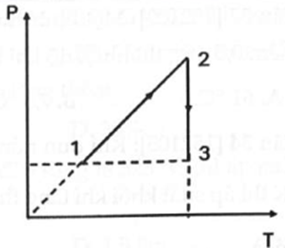
Sau quá trình biến đổi đẳng tích: \[\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \Rightarrow \frac{1}{{327 + 273}} = \frac{{{p_2}}}{{27 + 273}} \Rightarrow {p_2} = 2\,atm\]
Sau quá trình biến đổi đẳng áp: \[\frac{{{V_2}}}{{{T_2}}} = \frac{{{V_3}}}{{{T_3}}} \Rightarrow \frac{5}{{327 + 273}} = \frac{{{V_3}}}{{327 + 120 + 273}} \Rightarrow {V_3} = 6\] lít
Chọn C.
Lời giải
\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow \frac{{0,03.\frac{4}{3}\pi {{.10}^3}}}{{200}} = \frac{{1.\frac{4}{3}\pi R_2^3}}{{300}} \Rightarrow {R_2} = 3,56\,m\].Chọn A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Áp suất, thể tích và nhiệt độ của khí.
B. Khối lượng, thể tích và nhiệt độ của khí.
C. Áp suất, nhiệt độ và số mol của khí.
D. Khối lượng áp suất và số mol của khí.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo