Hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\). Góc đối đỉnh với \[\widehat {yOx'}\] là
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
![Hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\). Góc đối đỉnh với \[\widehat {yOx'}\] là A. \[\widehat {y'Ox'}\]. B. \[\widehat {y'Ox}\]. C. \[\widehat {yOx'}\]. D. \[\widehat {yOx}\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/11-1758501585.png)
Ta có \[\widehat {yOx'} = \widehat {xOy'}\] (hai góc đối đỉnh).
Do đó, chọn đáp án B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Số đối của \[ - \frac{1}{4}\] là \[ - \left( { - \frac{1}{4}} \right) = \frac{1}{4}\].
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Nhận thấy \(\frac{5}{3} = 1 + \frac{1}{3}\). Do đó, \(\frac{5}{3}\) được biểu diễn ở trục số đáp án C là đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

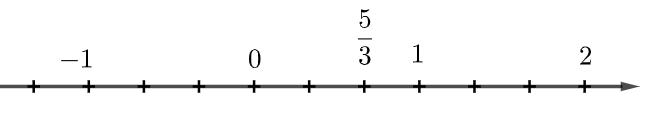



![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1758501867.png)
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1758501878.png)
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/09/16-1758501890.png)
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/09/17-1758501901.png)