Cho tam giác \[ABC\] cân tại \[A\] có \[\widehat {BAC} = 20^\circ \]. Trên cạnh \[AB\] lấy điểm \[D\] sao cho \[AD = BC.\] Số đo của góc \[BDC\] là
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
![Cho tam giác \[ABC\] cân tại \[A\] có \[\widehat {BAC} = 20^\circ \]. Trên cạnh \[AB\] lấy điểm \[D\] sao cho \[AD = BC.\] Số đo của góc \[BDC\] là A. \[30^\circ \]. B. \[70^\circ \]. C. \[75^\circ \]. D. \[80^\circ \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/11-1758587929.png)
Vẽ tam giác đều \(EBC\).
Ta có: \(BC = CE = EB\)
Mà \(AD = BC\) (gt)
Nên \(AD = BE\).
Chứng minh \(\Delta AEB = \Delta AEC\) (c.c.c) suy ra \(\widehat {DAB} = \widehat {DAC}\), do đó \(\widehat {EAB} = \frac{{20^\circ }}{2} = 10^\circ \).
\(\Delta ABC\) cân tại A, mà \(\widehat A = 20^\circ \) (gt) suy ra \(\widehat {ABC} = \left( {180^\circ - 20^\circ } \right):2 = 80^\circ \)
\(\Delta EBC\)đều nên \(\widehat {EBC} = 60^\circ \), tia \(BE\)nằm giữa hai tia \(BA,BC\) suy ra \(\widehat {ABE} = 80^\circ - 60^\circ = 20^\circ \)
Xét \(\Delta ABE\)và \(\Delta BAD\)có \(AB\) cạnh chung; \(\widehat {ABE} = \widehat {BAD} = 20^\circ ;BE = AD\)
Vậy \(\Delta ABE = \Delta BAD\) (c.g.c) suy ra \(\widehat {BAE} = \widehat {ABD} = 10^\circ \)
Mà \(\widehat {BDC} = \widehat {BAD} + \widehat {ABD}\) (góc ngoài của \(\Delta ABD\))
Nên \(\widehat {BDC} = 20^\circ + 10^\circ = 30^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
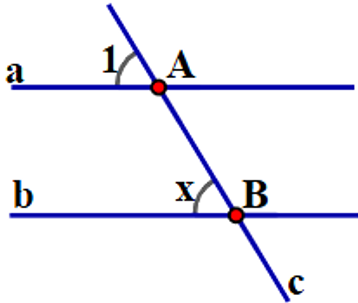
Ta có: \(a\parallel b\) nên \(\widehat {{A_1}} = \widehat {bBA} = 60^\circ \) (hai góc đồng vị).
Do đó, \(x = 60^\circ .\)
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Phát biểu Tiên đề Euclid: “Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó”.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.