Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao \(AB = 70\) m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi có độ cao so với mặt đất là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị).
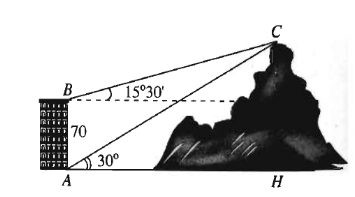
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao \(AB = 70\) m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi có độ cao so với mặt đất là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Từ giả thiết ta suy ra tam giác ABC có \(\widehat {CAB} = 60^\circ ,\widehat {ABC} = 105^\circ 30'\) và \(c = 70\).
Khi đó \(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - 165^\circ 30' = 14^\circ 30'\).
Theo định lí sin, ta có \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)\( \Leftrightarrow \frac{{AC}}{{\sin 105^\circ 30'}} = \frac{{70}}{{\sin 14^\circ 30'}}\)\( \Rightarrow AC = \frac{{70.\sin 105^\circ 30'}}{{\sin 14^\circ 30'}} \approx 269,4\).
Gọi CH là khoảng cách từ C đến mặt đất.
Tam giác vuông ACH có cạnh CH đối diện với góc 30° nên \(CH = \frac{{AC}}{2} = \frac{{269,4}}{2} = 134,7 \approx 135\) m.
Trả lời: 135.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
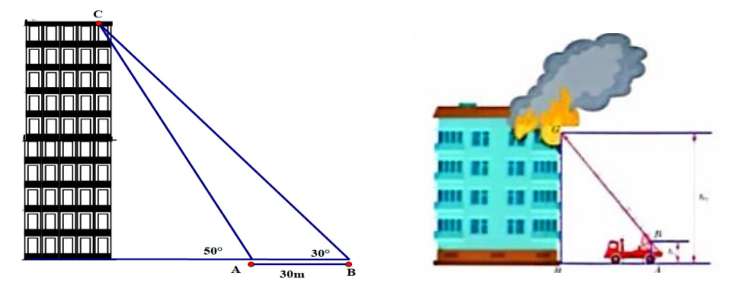
a) Xét tam giác ABC có \(\widehat {BAC} = 180^\circ - 50^\circ = 130^\circ ,\widehat {ABC} = 30^\circ \) nên \(\widehat {ACB} = 180^\circ - 130^\circ - 30^\circ = 20^\circ \).
b) Áp dụng định lí sin cho tam giác ABC ta được
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\) \( \Rightarrow \frac{{30}}{{\sin 20^\circ }} = \frac{{AC}}{{\sin 30^\circ }}\) \( \Rightarrow AC = \frac{{30.\sin 30^\circ }}{{\sin 20^\circ }} \approx 43,9\) m.
c) Xét tam giác vuông CHA vuông tại H nên \(CH = AC.\sin 50^\circ \approx 33,6\) m.
d) Chân thang cách mặt đất 1,8 m ta có CK = CH – HK = 33,6 – 1,8 = 31,8 m.
Khi đó khoảng cách tới chân tòa nhà xa nhất có thể là:
\(KD = \sqrt {C{D^2} - C{K^2}} = \sqrt {{{40}^2} - 31,{8^2}} \approx 24,3\) m.
Đáp án: a) Sai; b) Đúng; c) Sai; d) Sai.
Câu 2
A. \(2\).
B. \(\frac{1}{2}\).
C. \(1\).
D. \(\sqrt 2 \).
Lời giải
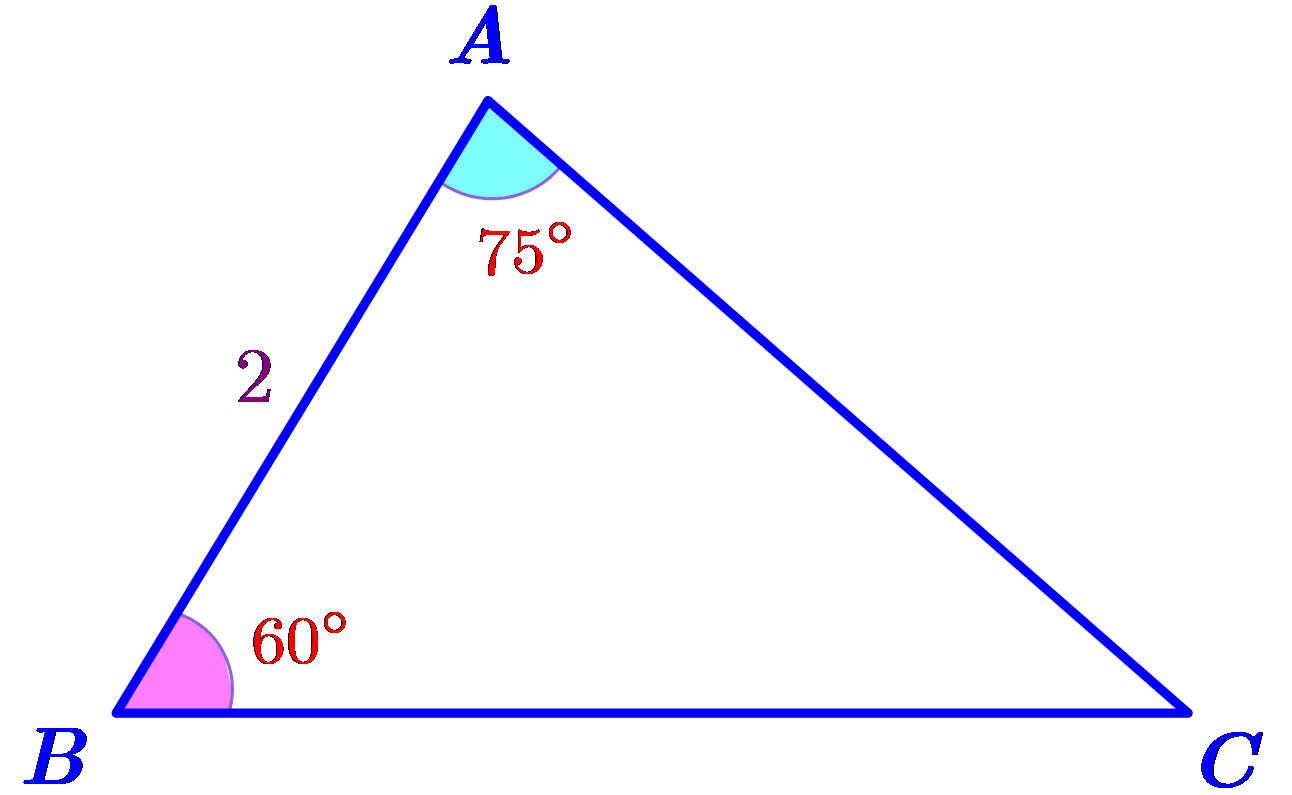
![Cho tam giác \(ABC\) có \(AB = 3\), \(BC = 5\) và độ dài đường trung tuyến \(BM = \sqrt {13} \). Bán kính \(r\) của đường tròn nội tiếp \[\Delta ABC\] bằng A. \(2\). B. \(\frac{1}{2}\). C. \(1\). D. \(\sqrt 2 \). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1758691234.png)
Có \(B{M^2} = \frac{{A{B^2} + B{C^2}}}{2} - \frac{{A{C^2}}}{4}\)\( \Rightarrow A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - 4B{M^2} = 2\left( {9 + 25} \right) - 4.13 = 16 \Rightarrow AC = 4\).
Có \(p = \frac{{3 + 4 + 5}}{2} = 6\).
\(S = \sqrt {6.\left( {6 - 3} \right).\left( {6 - 4} \right).\left( {6 - 5} \right)} = 6.r\)\( \Leftrightarrow r = \frac{6}{6} = 1\). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\widehat A = 90^\circ \).
B. \(\widehat A = 60^\circ \).
C. \(\widehat A = 30^\circ \).
D. \(\widehat A = 45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(2,37\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
B. \(0,63\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
C. \(2,45\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
D. \(1,58\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo