Một chất điểm đứng yên dưới tác dụng của ba lực \[{\overrightarrow F _1},\] \[{\overrightarrow F _2}\] và \[{\overrightarrow F _3}\] có độ lớn lần lượt là \[{F_1} = 4\,N,\] \[{F_2} = 5\,N\] và \[{F_3} = 6\,N.\] Hợp lực của hai lực \[{\overrightarrow F _1},\] \[{\overrightarrow F _2}\] có độ lớn bằng
Quảng cáo
Trả lời:
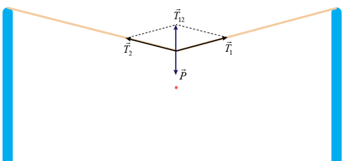
Theo điều kiện cân bằng của chất điểm ta có: \[{\overrightarrow F _1} + {\overrightarrow F _2} + {\overrightarrow F _3} = \overrightarrow 0 \Rightarrow {\overrightarrow F _1} + {\overrightarrow F _2} = - {\overrightarrow F _3}\] hay \[{\overrightarrow F _{12}} = - {\overrightarrow F _3}\,\,\left( * \right)\]
Từ \[\left( * \right)\] ta có nhận xét: \[\left\{ \begin{array}{l}{\overrightarrow F _{12}} \uparrow \downarrow {\overrightarrow F _3}\,\\{F_{12}} = {F_3} = 6\,N\end{array} \right.\]
chọn C
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Đáp án: |
4 |
, |
9 |
|
Hướng dẫn giải
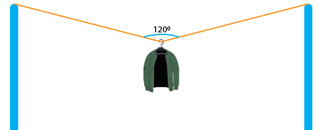
Vì chiếc áo đang nằm cân bằng nên: \({\vec T_1} + {\vec T_2} + \vec P = \vec 0\)
- Điểm treo áo nằm chính giữa dây, do đó:\({T_1} = {T_2} = T\)
- Độ lớn hợp lực của \({\vec T_1}\) và \({\vec T_2}\) là: \({T_{12}} = 2T\cos \frac{{{{120}^0}}}{2} = 2T\cos {60^0}\)
- Từ điều kiện cân bằng, ta có: \({T_{12}} = P = 2T\cos {60^0} \Rightarrow T = \frac{{mg}}{{2 \cdot \cos {{60}^0}}} = \frac{{0,5 \cdot 9,8}}{{2 \cdot \cos {{60}^0}}} \approx 4,9N\)
Câu 2
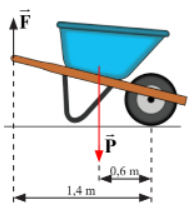
A. khoảng cách từ O đến điểm đặt của lực F.
B. khoảng cách từ O đến ngọn của vec tơ lực F.
Lời giải
chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.