Hình bên mô tả cửa xếp tự động. Mỗi khung Hình a được nối bởi các thanh inox có dạng hình thoi cạnh 30 cm.
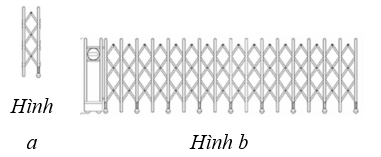
a) Hỏi mỗi khung như Hình a cần bao nhiêu mét thanh inox để nối?
b) Hỏi cửa xếp tự động ở Hình b cần bao nhiêu mét thanh inox để nối?
Hình bên mô tả cửa xếp tự động. Mỗi khung Hình a được nối bởi các thanh inox có dạng hình thoi cạnh 30 cm.

b) Hỏi cửa xếp tự động ở Hình b cần bao nhiêu mét thanh inox để nối?
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Mỗi khung Hình a được nối bởi 2 hình thoi và thêm hai cạnh của 1 hình thoi cùng kích thước.
Như vậy, mỗi khung như Hình a cần số mét thanh inox để nối là: \(4 \cdot 30 + 2 \cdot 30 = 180{\rm{\;(cm)}}{\rm{.}}\)
b) Ta thấy Hình b có 16 khung như Hình a nên cửa xếp tự động như Hình b cần số mét thanh inox để nối là: \[16 \cdot 180 = 2\,\,880{\rm{\;(cm)}}{\rm{.}}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Diện tích ban đầu của sân nhà bác Cường là: \(6 \cdot 4 = 24{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
b) Diện tích phần sân mở rộng là: \[2 \cdot \frac{{1 \cdot 4}}{2} = 4{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Số tiền bác Cường phải trả để lát hết sân mới là: \(\left( {24 + 4} \right) \cdot 140\,\,000 = 3\,\,920\,\,000\) (đồng).
Lời giải
Hướng dẫn giải
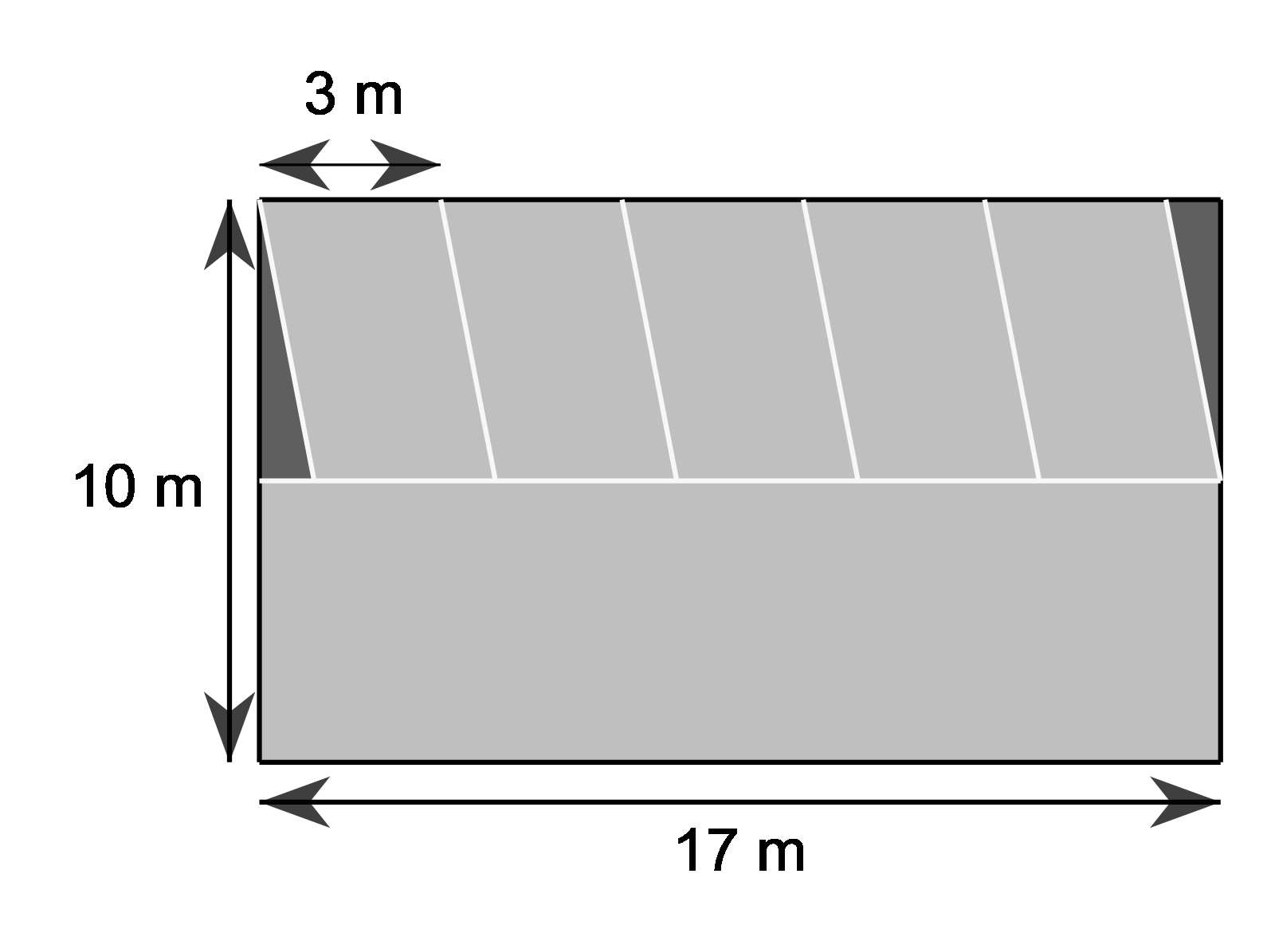
a) Mỗi chỗ đậu xe có dạng là một hình bình hành với độ dài 1 cạnh là 3 m và chiều cao tương ứng là \(10:2 = 5{\rm{\;(m)}}{\rm{.}}\)
Vậy diện tích chỗ đậu xe dành cho một ô tô là: \(3 \cdot 5 = 15{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
b) Diện tích cho 5 chỗ đậu ô tô là: \(5 \cdot 15 = 75{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích phần quay đầu xe là: \(17 \cdot 5 = 85{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích dành cho đậu xe và quay đầu xe là: \(75 + 85 = 160{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Sân nhà bác Cường có dạng hình chữ nhật với chiều dài và chiều rộng lầng lượt là \[{\rm{6\;m}}\] và \(4{\rm{\;m}}\). Bác Cường muốn mở rộng sân sang hai bên như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/15-1761292650.png)