Một khu đất hình thang cân \[ABCD\] có độ dài các cạnh đáy lần lượt là 30 m và 36 m và chiều cao là 25 m. Trong khu đất đó, người ta đào một cái ao hình vuông \[EFGH\] như hình vẽ, phần đất còn lại trồng hoa.
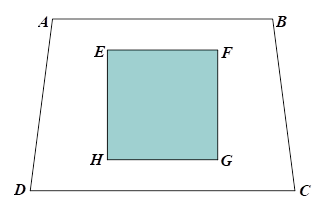
a) Tính diện tích phần đất trồng hoa, biết \[EF\] = 15 m.
b) Để giữ bờ, người ta trồng cây xung quanh bờ ao, biết rằng cây đầu tiên trồng ở điểm \[E\] và cứ 3 m thì người ta trồng một cây. Hỏi quanh bờ ao, trồng được bao nhiêu cây?
Một khu đất hình thang cân \[ABCD\] có độ dài các cạnh đáy lần lượt là 30 m và 36 m và chiều cao là 25 m. Trong khu đất đó, người ta đào một cái ao hình vuông \[EFGH\] như hình vẽ, phần đất còn lại trồng hoa.
a) Tính diện tích phần đất trồng hoa, biết \[EF\] = 15 m.
b) Để giữ bờ, người ta trồng cây xung quanh bờ ao, biết rằng cây đầu tiên trồng ở điểm \[E\] và cứ 3 m thì người ta trồng một cây. Hỏi quanh bờ ao, trồng được bao nhiêu cây?
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều cấu trúc mới có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Diện tích khu đất hình thang cân \[ABCD\] là: \[\frac{1}{2}\left( {30 + 36} \right) \cdot 25 = 825\] (m2).
Diện tích cái ao hình vuông \[EFGH\] là: \[{15^2} = 225\] (m2).
Diện tích phần đất trồng hoa là: \[825 - 225 = 600\](m2).
b) Do độ dài cạnh hình vuông \[EFGH\] là 15 m, mà 15 chia hết cho 3 và \(15:3 = 5\) nên ở mỗi đỉnh của hình vuông đều có một cây và trên mỗi cạnh trồng được 5 cây.
Cách 1: Như vậy, trên 4 cạnh sẽ trồng được \(4 \cdot 5 = 20\) (cây).
Tuy nhiên, mỗi cây ở mỗi đỉnh đã được tính 2 lần nên số cây thực tế trồng được là: \(20 - 4 = 16\) (cây).
Cách 2: Như vậy, trên mỗi cạnh, nếu không tính 2 cây trồng ở hai đỉnh thì sẽ trồng thêm được \(5 - 2 = 3\) (cây).
Trên 4 cạnh, không tính cây trồng được ở các đỉnh, sẽ trồng được \(4 \cdot 3 = 12\) (cây).
Khi đó, số cây thực tế trồng được là: \(12 + 4 = 16\) (cây).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có:
\(A = {1000^0} + {1000^{1001}} + {1000^{1002}} + {1000^{1003}} + {1000^{1004}}\)
\( = 1 + \left( {{{1000}^{1001}} + {{1000}^{1002}}} \right) + \left( {{{1000}^{1003}} + {{1000}^{1004}}} \right)\)
\( = 1 + {1000^{1001}} \cdot \left( {1 + 1000} \right) + {1000^{1003}} \cdot \left( {1 + 1000} \right)\)
\( = 1 + {1000^{1001}} \cdot 1001 + {1000^{1003}} \cdot 1001\)
\[ = 1 + 1001 \cdot \left( {{{1000}^{1001}} + {{1000}^{1003}}} \right).\]
Ta thấy rằng \[1001 \cdot \left( {{{1000}^{1001}} + {{1000}^{1003}}} \right)\,\, \vdots \,\,1001\] nên \[1 + 1001 \cdot \left( {{{1000}^{1001}} + {{1000}^{1003}}} \right)\] chia 1001 dư 1.
Vậy \(A:1001\) có số dư bằng 1.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp số: 16.
Gọi \(a\) (cm) \(\left( {a > 0} \right)\) là độ dài cạnh của hình vuông.
Khi đó, diện tích của hình vuông đó là: \(a \cdot a = {a^2}\) (cm2).
Theo bài, ta có:
\({a^2} = 16\)
\({a^2} = {4^2}\)
Suy ra \(a = 4\) (do \(a > 0).\)
Do đó, độ dài cạnh của hình vuông đã cho là 4 cm.
Vậy, chu vi của hình vuông đó là: \[4 \cdot 4 = 16\] (cm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập