Một vật nhỏ khối lượng 100g dao động theo phương trình \(x = 8{\rm{cos10t}}\) (x tính bằng cm, t tính bằng s). Động năng cực đại của vật bằng
A. 32 mJ.
B. 64 mJ.
C. 16 mJ.
D. 128 mJ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Động năng cực đại là:
Thay số vào, ta được:
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi phương trình dao động của vật có dạng: \(x = Ac{\rm{os}}(\omega t + \varphi )\)
Khi đó phương trình vận tốc và gia tốc có biểu thức lần lượt là:
\(v = - A\omega \sin (\omega t + \varphi )\)
\(a = - A{\omega ^2}c{\rm{os}}(\omega t + \varphi )\)
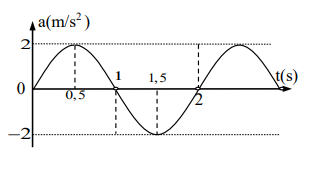
Từ đồ thị, ta có:
+ Theo trục hoành ta có thời gian để có một hình sin là 2(s) \( \Rightarrow \) Chu kì của dao động:
\(T = 2s \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{2}\pi {\rm{ (rad/s)}}\)
+ Theo trục tung ta có gia tốc đạt giá trị lớn nhất là \(2{\rm{ m/}}{{\rm{s}}^2}\):
\({a_{ma{\rm{x}}}} = A{\omega ^2} \Rightarrow A = \frac{{{a_{ma{\rm{x}}}}}}{{{\omega ^2}}} = \frac{{200}}{{{\pi ^2}}} = 20cm\)
+ Khi t = 0 thì a = 0 và gia tốc đang tăng \( \Rightarrow \)li độ x = 0 và đang đi theo chiều âm (vì x và a ngược pha) \( \Rightarrow \) Pha ban đầu của x là: \(\varphi = \frac{\pi }{2}\)(rad)
Vậy phương trình dao động của vật là: \(x = 20c{\rm{os}}(\pi t + \frac{\pi }{2}){\rm{ (cm)}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\sqrt {\frac{m}{k}} \).
B. \(2\pi \sqrt {\frac{k}{m}} \).
C. \(\sqrt {\frac{k}{m}} \).
D. \(\frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Chu kì của lực cưỡng bức lớn hơn chu kì dao động riêng của hệ dao động.
B. Tần số của lực cưỡng bức lớn hơn tần số dao động riêng của hệ dao động.
C. Tần số của lực cưỡng bức bằng tần số dao động riêng của hệ dao động.
D. Chu kì của lực cưỡng bức nhỏ hơn chu kì dao động riêng của hệ dao động.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo