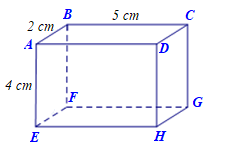
Cho góc bẹt \(xOy\). Vẽ ba tia \(Om,\,\,On,\,\,Oz\) sao cho tia \(Om\) nằm giữa hai tia \[Ox,\,\,Oz\] và \(\widehat {xOm} = 50^\circ ,\,\,\widehat {xOz} = 130^\circ \). Vẽ tia \(On\) là tia đối của tia \(Oz\).
(a) Vẽ hình và kể tên các góc kề bù với góc \(xOz\) có trong hình vẽ.
(b) Tính số đo của góc \(yOz\). Giải thích tại sao tia \[Ox\] là tia phân giác của góc \(mOn\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Học sinh vẽ hình đúng số đo góc.
Góc kề bù với góc \(xOz\) là \(\widehat {yOz}\) và \(\widehat {xOn}\).
b) Ta có \(\widehat {xOz} + \widehat {yOz} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {yOz} = 180^\circ - \widehat {xOz} = 180^\circ - 130^\circ = 50^\circ \)
Lại có \(\widehat {xOn} = \widehat {yOz} = 50^\circ \) (hai góc đối đỉnh)
Do tia \(Ox\) nằm giữa hai tia \(Om,\,\,On\) và \(\widehat {xOn} = \widehat {xOm} = 50^\circ \) nên tia \(Ox\) là tia phân giác của góc \(mOn\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
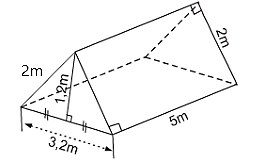
Diện tích xung quanh của lều tại là:
\({S_{xq}} = \left( {2 + 2 + 3,2} \right)\,\,.\,\,5 = 36\) (m2)
Diện tích đáy là:
\({S_d} = 2.\frac{1}{2}\,\,.\,\,1,2\,\,.\,\,3,2 = 3,84\)(m2)
Diện tích vải cần mua để dựng lều là:
\(36 + 3,84 = 39,84\)(m2)
Số tiền cần để mua vải là:
\(39,84\,\,.\,\,150{\rm{ }}000 = 5{\rm{ }}976{\rm{ }}000\) (đồng)
Vì \(6{\rm{ 000 000 > 5 976 000}}\) nên nhóm học sinh đủ tiền mua vải.
Lời giải
Đáp án đúng là: D
Hai số đối nhau có tổng bằng 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\[CD = 2{\rm{ cm}}\]
\(HG = 4\,\,{\rm{cm}}\)
\(GF = 5\,\,{\rm{cm}}\)
\(DH = 4\,\,{\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.