Một trường THCS tổ chức cho học sinh đi trải nghiệm thực tế ở nhà máy thủy điện Hoà Bình. Sau khi học sinh đăng kí, ban tổ chức tính toán và thấy rằng nếu xếp mỗi xe 36 học sinh, 40 học sinh hay 45 học sinh đều vừa đủ. Tính số học sinh đi trải nghiệm biết rằng số học sinh tham gia trong khoảng 1 000 đến 1 100 học sinh.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Gọi \(x\) (học sinh) là số học sinh của trường THCS \(\left( {x \in {\mathbb{N}^*};\,\,1\,\,000 < x < 1\,\,100} \right)\).
Vì khi xếp mỗi xe 36 học sinh thì vừa đủ nên \[x \in B\left( {36} \right)\];
Vì khi xếp mỗi xe 40 học sinh thì vừa đủ nên \[x \in B\left( {40} \right)\];
Vì khi xếp mỗi xe 45 học sinh thì vừa đủ nên \[x \in B\left( {45} \right)\].
Do đó \(x \in BC\left( {36\,,\,\,40\,,\,\,45} \right)\).
Ta có: \(36 = 2\,.\,2\,.\,3\,.\,3 = {2^2}\,.\,{3^2}\);
\(40 = 2\,.\,2\,.\,2\,.\,5 = {2^3}\,.\,5\);
\(45 = 3\,.\,3\,.\,5 = {3^2}\,.\,5\).
Khi đó \(BCNN\left( {36\,,\,\,40\,,\,\,45} \right) = {2^3}\,.\,{3^2}\,.\,5 = 8\,.\,9\,.\,5 = 360\).
Do đó \(BC\left( {36\,,\,\,40\,,\,\,45} \right) = \left\{ {0\,;\,\,360\,;\,\,720\,;\,\,1080\,;\,\,1440\,;\,\,...} \right\}\).
Vì \[100 < x < 1100\] nên \[x = 1080\].
Vậy trường THCS đó có 1080 học sinh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \(A = 1 + 4 + {4^2} + {4^3} + ... + {4^{2021}}\)
\[ = (1 + 4 + {4^2}) + ({4^3} + {4^4} + {4^5}) + ... + ({4^{2019}} + {4^{2020}} + {4^{2021}})\]
\[ = (1 + 4 + {4^2}) + {4^3}(1 + 4 + {4^2}) + ... + {4^{2019}}(1 + 4 + {4^2})\]
\[ = 21\,\,.\,\,(1 + {4^3} + ... + {4^{2019}})\].
Vì \(21\,\, \vdots \,\,21\) nên \[A = 21\,\,.\,\,(1 + {4^3} + ... + {4^{2019}})\, \vdots \,\,21\].
Vậy \(A = 1 + 4 + {4^2} + {4^3} + ... + {4^{2021}}\) chia hết cho 21.
Lời giải
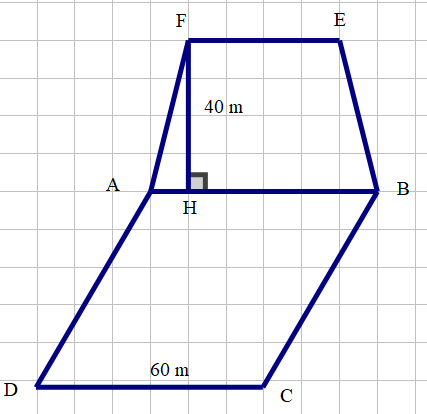
Chu vi của mảnh đất hình thoi \[ABCD\] là:
\(60\,\,.\,\,4 = 240\) (m)
Vậy chu vi của mảnh đất hình thoi \[ABCD\] bằng 240 m.
Độ dài đáy \(EF\) bằng:
\(EF = AB - 20 = 60 - 20 = 40\) (m)
Diện tích cái ao hình thang cân \[ABEF\] bằng:
\(\frac{{60 + 40}}{2}\,\,.\,\,40 = 2\,\,000\,\)(m2).
Vậy diện tích cái ao hình thang cân \[ABEF\] bằng \(2\,\,000\,\)m2.
Câu 3
\[AB\] song song với \[CD\] và \[BC\] song song với \[AD\]
\[AB = BC = CD = AD\]
\[AC\] và \[BD\] vuông góc với nhau
Bốn góc đỉnh \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\] bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\[\left( {a + b + c} \right)\,\, \vdots \,\,2\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,5\]
\[\left( {a + b + c} \right)\,\,\cancel{ \vdots }\,\,5\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,25\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.