Trong các đơn thức sau, đơn thức nào đồng dạng với đơn thức \( - 3{x^2}yz\)?
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B
Đơn thức \(\frac{2}{3}{x^2}yz\) đồng dạng với đơn thức \( - 3{x^2}yz\) vì hai đơn thức này đều có hệ số khác 0 và có cùng phần biến là \({x^2}yz\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
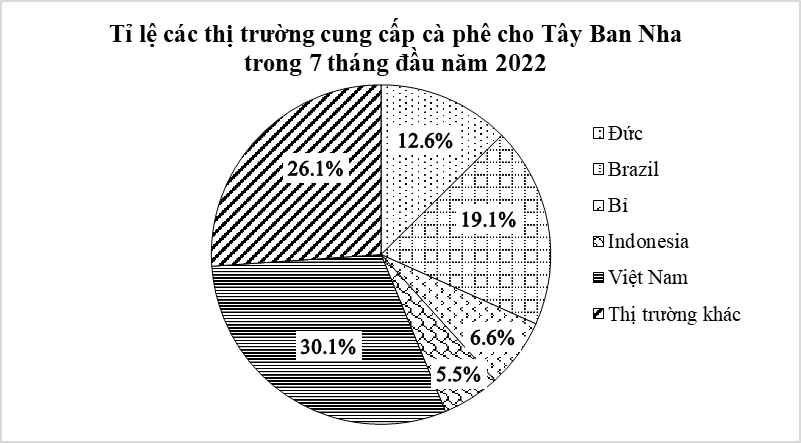
a) Trong 7 tháng đầu năm 2022 thị trường cung cấp cà phê cho Tây Ban Nha nhiều nhất là thị trường Việt Nam \((30,1\% )\); ít nhất là thị trường Indonesia \((5,5\% )\).
b) Các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022:
Lượng cà phê thị trường Đức cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,12,6\% = 28\,\,092,456\] (tấn)
Lượng cà phê thị trường Brazil cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,19,1\% = 42\,\,584,596\] (tấn)
Lượng cà phê thị trường Bỉ cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,6,6\% = 14\,\,715,096\] (tấn)
Lượng cà phê thị trường Indonesia cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,5,5\% = 12\,\,262,58\] (tấn)
Lượng cà phê thị trường Việt Nam cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,30,1\% = 67\,\,109,756\] (tấn)
Lượng cà phê thị trường khác cung cấp cà phê cho Tây Ban Nha là:
\[222\,\,956\,\,.\,\,26,1\% = 58\,\,191,516\] (tấn)
Từ đó, ta có bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 như sau:
|
Thị trường |
Đức |
Brazil |
Bỉ |
Indonesia |
Việt Nam |
Khác |
|
Lượng cà phê (tấn) |
\[28\,\,092,456\] |
\[42\,\,584,596\] |
\[14\,\,715,096\] |
\[12\,\,262,58\] |
\[67\,\,109,756\] |
\[58\,\,191,516\] |
c) Thị trường Indonesia và Bỉ là hai thị trường cung cấp lượng cà phê ít nhất cho Tây Ban Nha trong 7 tháng đầu năm 2022.
Việt Nam cung cấp cà phê cho Tây Ban Nha nhiều hơn \[24,6\% \] so với thị trường Indonesia (vì \[30,1\% - 5,5\% = 24,6\% \]).
Theo em, bài báo nêu thông tin chính xác.
Lời giải
Hướng dẫn giải:
![Cho tam giác \[ABC\] vuông tại \[A\] có (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/5-1763728585.png)
a) Vì \(\Delta ABC\) vuông tại \(A\) nên \(\widehat {BAC} = 90^\circ \) hay \(\widehat {DAE} = 90^\circ \).
Ta có \(HD \bot AB\); \(HE \bot AC\) nên \(\widehat {HDA} = 90^\circ \); \(\widehat {HEA} = 90^\circ \).
Tứ giác \(ADHE\) có \[\widehat {DAE} = \widehat {HDA} = \widehat {HEA} = 90^\circ \].
Do đó, tứ giác \(ADHE\) là hình chữ nhật.
b) Xét \(\Delta AHD\) vuông tại \(D\), áp dụng định lý Pythagore, ta có:
\(A{H^2} = A{D^2} + D{H^2}\) hay \(25 = 16 + D{H^2}\).
Suy ra \(D{H^2} = 9\) nên \(DH = 3\,\,{\rm{cm}}\).
Tứ giác \(ADHE\) là hình chữ nhật nên ta có
\({S_{ADHE}} = AD\,.\,DH = 4\,.\,3 = 12\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy diện tích tứ giác \(ADHE\) bằng \(12\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
c) Theo đề bài, \(D\) là trung điểm của \(BI\) và \(D\) cũng là trung điểm của \(HK.\)
Khi đó, hai đường chéo \(BI\) và \(HK\) cắt nhau tại trung điểm của mỗi đường.
Do đó, tứ giác \(BKIH\) là hình bình hành.
Hình bình hành \(BKIH\) có hai đường chéo \(BI\) và \(HK\) vuông góc với nhau nên tứ giác \[BKIH\] là hình thoi.
Mà \(AH \bot BH\) suy ra \(KI \bot AH\).
Xét \(\Delta AHK\) có \(AD \bot KH;\,\,KI \bot AH\) và \(AD\) cắt \(KI\) tại \(I\).
Do đó, \(I\) là trực tâm của tam giác \(AKH\) suy ra \(HI \bot AK\) (đpcm).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.