Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Với mọi số nguyên \(n\) ta có: \(\left( {3n + 1} \right) \vdots \left( {2n - 1} \right)\)
Suy ra \(2\left( {3n + 1} \right) \vdots \left( {2n - 1} \right)\)
Hay \(\left( {6n + 2} \right) \vdots \left( {2n - 1} \right)\)
\(\left( {6n - 3 + 5} \right) \vdots \left( {2n - 1} \right)\)
\(\left[ {3\left( {2n - 1} \right) + 5} \right] \vdots \left( {2n - 1} \right)\)
Suy ra \(5 \vdots \left( {2n - 1} \right)\) hay \(2n - 1 \in \)Ư\(\left( 5 \right) = \left\{ { - 5; - 1;1;5} \right\}\)
Ta có bảng sau:
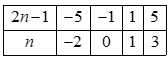
Thử lại:
• Với \(n = - 2\) ta có \(3n + 1 = - 5\) và \(2n - 1 = - 5\), do đó \(\left( {3n + 1} \right) \vdots \left( {2n - 1} \right)\)
Suy ra \(n = - 2\) thỏa mãn yêu cầu.
• Với \(n = 0\) ta có \(3n + 1 = 1\) và \(2n - 1 = - 1\), do đó \(\left( {3n + 1} \right) \vdots \left( {2n - 1} \right)\)
Suy ra \(n = 0\) thỏa mãn yêu cầu.
• Với \(n = 1\) ta có \(3n + 1 = 4\) và \(2n - 1 = 1\), do đó \(\left( {3n + 1} \right) \vdots \left( {2n - 1} \right)\)
Suy ra \(n = 1\) thỏa mãn yêu cầu.
• Với \(n = 3\) ta có \(3n + 1 = 10\) và \(2n - 1 = 5\), do đó \(\left( {3n + 1} \right) \vdots \left( {2n - 1} \right)\)
Suy ra \(n = 3\) thỏa mãn yêu cầu.
Vậy \(n \in \left\{ { - 2;0;1;3} \right\}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \[x\] là số bánh ngọt của cửa hàng (chiếc, \(x \in \mathbb{N}*;\,\,100 \le x \le 150\))
Vì nếu xếp số bánh ngọt vào các túi, mỗi túi 10 chiếc, 12 chiếc, 15 chiếc đều vừa đủ nên\(x \vdots 10,x \vdots 12,x \vdots 15\).
Suy ra \(x\) là \(BC\left( {10,12,15} \right)\)
Ta có: \(10 = 2.5;\,\,\,\,12 = {2^2}.3;\,\,\,15 = 3.5\)
Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\)
Suy ra \(BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;...} \right\}\)
Mà \(100 \le x \le 150\) nên \(x = 120\)
Vậy cửa hàng có 120 chiếc bánh ngọt.
Lời giải
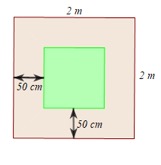
Đổi \(2\,\,{\rm{m}} = 200\,\,{\rm{cm}}\).
a) Cạnh của bồn hoa thu nhỏ dạng hình vuông là:
\(200 - 50 - 50 = 100\,\,\left( {{\rm{cm}}} \right)\).
Diện tích của bồn hoa sau khi thu nhỏ là:
\(100.100 = 10\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích của bồn hoa lúc đầu khi chưa thu nhỏ là:
\(200.200 = 40\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích của lối đi là:
\[40\,\,000 - \,\,10\,\,000 = 30\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Chữ H, chữ I và chữ A;
B. Chữ H, chữ I và chữ N;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Biển báo R122 (Dừng lại) có hình lục giác đều;
B. Biển báo 437 (Đường cao tốc) có hình vuông;
C. Biển báo 207a (Giao nhau với đường không ưu tiên) có hình tam giác đều;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.