Trên đường thẳng \[xy\] lấy một điểm \[O.\] Trên tia \[Ox\] lấy điểm \[A\] sao cho \(OA = 3{\rm{\;cm}}.\) Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB = 3{\rm{\;cm}}.\) Trên tia \(Oy\) lấy điểm \(C\) sao cho \(OC = a{\rm{\;(cm)}}\) với \(0 < a < 3.\) Khi đó:
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) Đ. b) Đ. c) S. d) Đ.

a) Vì tia \(OA\) và tia \[OB\] là hai tia đối nhau nên \(O\) nằm giữa hai điểm \(A\) và \(B.\)
Lại có \(OA = OB\) (cùng bằng \(3{\rm{\;cm}})\)
Do đó \(O\) là trung điểm của đoạn thẳng \(AB.\)
Do đó, ý a) là đúng.
b) Có \(O\) là trung điểm của đoạn thẳng \(AB\) nên \(AB = OA + OB = 3 + 3 = 6\,\,\left( {{\rm{cm}}} \right)\).
Do đó, ý b) là đúng.
c) Vì điểm \(C\) nằm trên tia \(Oy\) sao cho \(OC = a{\rm{\;(cm)}}\) với \(0 < a < 3\) nên \(OC < OB\)
Do đó \(C\) nằm giữa hai điểm \(O\) và \(B.\)
Do đó, ý c) là sai.
d) Khi đó để \(C\) là trung điểm của đoạn thẳng \(OB\) thì cần thêm điều kiện
\[OC = CB = \frac{1}{2}OB = \frac{1}{2} \cdot 3 = 1,5{\rm{\;(cm)}}{\rm{.}}\]
Vậy \(a = 1,5{\rm{\;(cm)}}\) (thỏa mãn điều kiện).
Do đó, ý d) là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: 15
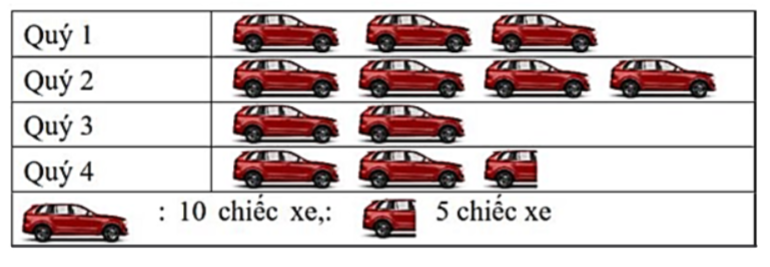
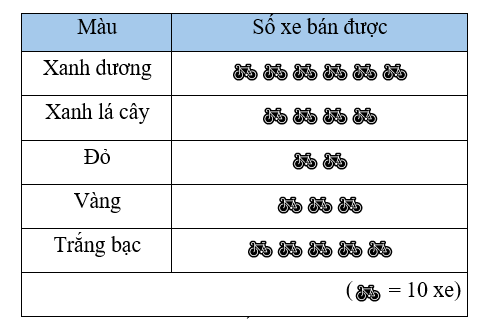
Số xe cửa hàng bán được ở Quý 2 là: \(10 \cdot 4 = 40\) (chiếc).
Số xe cửa hàng bán được ở Quý 4 là: \(10 \cdot 2 + 5 = 25\) (chiếc).
Quý 2 bán được nhiều hơn Quý 4 số xe là: \(40 - 25 = 15\) (chiếc).
Lời giải
Hướng dẫn giải
Đáp án: 30
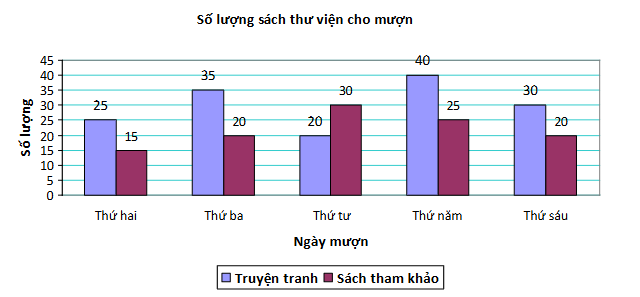
Tổng số truyện tranh mà học sinh đã mượn trong tuần là: \(25 + 35 + 20 + 40 + 30 = 150\) (quyển).
Tổng số sách tham khảo mà học sinh đã mượn là: \(15 + 20 + 30 + 25 + 20 = 120\) (quyển).
Số lượng truyện tranh được mượn trong tuần nhiều hơn số lượng sách tham khảo số quyển là:
\(150 - 120 = 30\) (quyển).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.