Vẽ được bao nhiêu đường thẳng từ 10 điểm phân biệt, trong đó không có 3 điểm nào thẳng hàng?
Vẽ được bao nhiêu đường thẳng từ 10 điểm phân biệt, trong đó không có 3 điểm nào thẳng hàng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(45\)
Lấy 1 điểm kết hợp với 9 điểm còn lại (không có ba điểm nào thẳng hàng) ta vẽ được 9 đường thẳng.
Do đó, qua 10 điểm phân biệt trong đó không có ba điểm nào thẳng hàng thì tạo được số đường thẳng là: \(10 \cdot 9 = 90\) (đường thẳng).
Nhưng mỗi đường thẳng được tính 2 lần nên số đường thẳng thực tế là: \(90:2 = 45\) (đường thẳng).
Vậy có tất cả 45 đường thẳng thỏa mãn yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
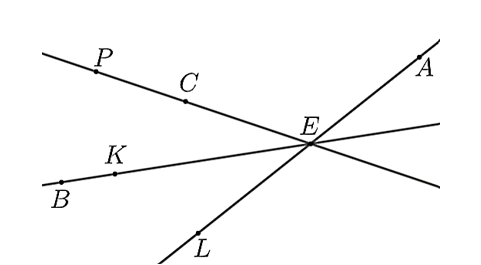
Đáp án: \(3\)
Có tất cả 3 bộ ba điểm thẳng hàng là: \(\left( {P,\;\,C,\;\,E} \right);\;\,\left( {B,\;\,K,\;\,E} \right);\;\,\left( {A,\;\,L,\;\,E} \right).\)
Vậy có tất cả 3 bộ ba điểm thẳng hàng trong hình vẽ trên.
Câu 2
A. 0 điểm.
B. 2 điểm.
C. 1 điểm.
D. 3 điểm.
Lời giải
Đáp án đúng là: C
Hai đường thẳng cắt nhau có duy nhất 1 điểm chung.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 1 đường thẳng.
B. 2 đường thẳng.
C. 3 đường thẳng.
D. 4 đường thẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập