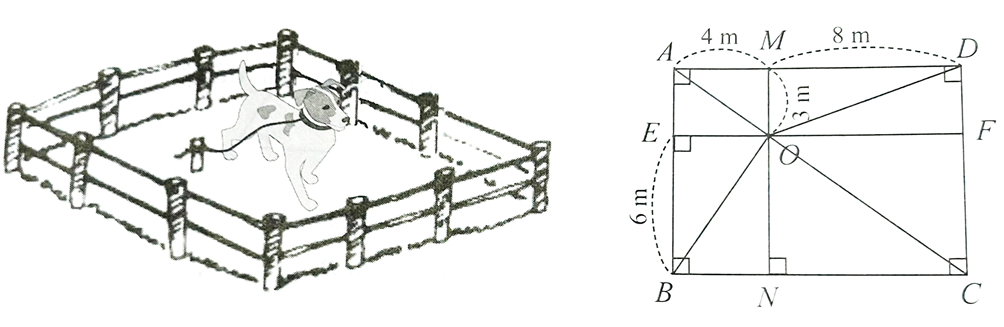
1) Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?

2) Cho tam giác \(ABC\) có ba góc nhọn, các đường cao \(AD,\) \(BE\) cắt nhau tại \(H.\)

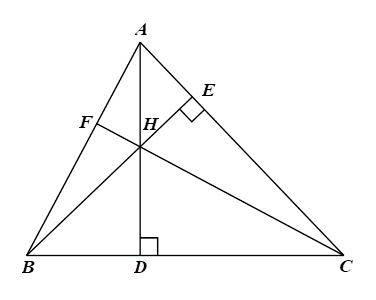
a) Chứng minh: $\Delta ADC\backsim \Delta BEC.$

b) Chứng minh: \[HE \cdot HB = HA \cdot HD.\]

c) Gọi \(F\) là giao điểm của \(CH\) và \(AB.\) Chứng minh: \[AF \cdot AB = AH \cdot AD.\]

d) Chứng minh: \(\frac{{HD}}{{AD}} + \frac{{HE}}{{BE}} + \frac{{HF}}{{CF}} = 1.\)

Hướng dẫn giải

Ta có: \(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)

\( = \frac{{{{\left( {a - 2} \right)}^3} + {{\left( {b - 2} \right)}^3} + {{\left( {c - 2} \right)}^3}}}{{\left( {a - 2} \right)\left( {b - 2} \right)\left( {c - 2} \right)}}\)

Đặt \(a - 2 = x;\,\,b - 2 = y;\,\,c - 2 = z.\)

Khi đó \(M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}}.\)

Mặt khác, từ \(a + b + c = 6\) suy ra \(\left( {a - 2} \right) + \left( {b - 2} \right) + \left( {c - 2} \right) = 0\)

Hay \(x + y + z = 0\)

Suy ra \(x + y =  - z\)

\[{\left( {x + y} \right)^3} = {\left( { - z} \right)^3}\]

\({x^3} + {y^3} + 3xy\left( {x + y} \right) =  - {z^3}\)

\({x^3} + {y^3} + 3xy\left( { - z} \right) =  - {z^3}\)

\({x^3} + {y^3} + {z^3} = 3xyz\)

Do đó \(M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}} = \frac{{3xyz}}{{xyz}} = 3.\)

Vậy \(M = 3.\)

Hướng dẫn giải

a) Điều kiện xác định của biểu thức \(M\) là \(\left\{ \begin{array}{l}{x^2} - 2x \ne 0\\x \ne 0\end{array} \right.,\) hay \(\left\{ \begin{array}{l}x\left( {x - 2} \right) \ne 0\\x \ne 0\end{array} \right.,\) tức là \(\left\{ \begin{array}{l}x \ne 0\\x - 2 \ne 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right..\)

b) Với \(x \ne 0\) và \(x \ne 2,\) ta có:

\[M = \frac{1}{{{x^2} - 2x}} \cdot \left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1 = \frac{1}{{x\left( {x - 2} \right)}} \cdot \left( {\frac{{{x^2} + 4}}{x} - \frac{{4x}}{x}} \right) + 1\]

\[ = \frac{1}{{x\left( {x - 2} \right)}} \cdot \frac{{{x^2} + 4 - 4x}}{x} + 1 = \frac{1}{{x\left( {x - 2} \right)}} \cdot \frac{{{{\left( {x - 2} \right)}^2}}}{x} + 1\]

\[ = \frac{{x - 2}}{{{x^2}}} + \frac{{{x^2}}}{{{x^2}}} = \frac{{{x^2} + x - 2}}{{{x^2}}}.\]

Vậy với \(x \ne 0\) và \(x \ne 2,\) thì \(M = \frac{{{x^2} + x - 2}}{{{x^2}}}.\)

Ta có \[\left| {4 - x} \right| = 2\]

Thay \[x = 6\] vào biểu thức \(M = \frac{{{x^2} + x - 2}}{{{x^2}}},\) ta được: \[M = \frac{{{6^2} + 6 - 2}}{{{6^2}}} = \frac{{36 + 6 - 2}}{{36}} = \frac{{10}}{9}.\]

Vậy \(M = \frac{{10}}{9}\) khi \[\left| {4 - x} \right| = 2.\]

c) Với \(x \ne 0\) và \(x \ne 2,\) ta có \[M = \frac{{{x^2} + x - 2}}{{{x^2}}} = 1 + \frac{1}{x} - \frac{2}{{{x^2}}}.\]

Đặt \[\frac{1}{x} = t\,\,\,\left( {t \ne 0;\,\,t \ne \frac{1}{2}} \right),\] khi đó:

\[M = 1 + t - 2{t^2} =  - 2\left( {{t^2} - \frac{1}{2}t - \frac{1}{2}} \right) =  - 2\left( {{t^2} - 2 \cdot t \cdot \frac{1}{4} + \frac{1}{{16}} - \frac{1}{2} - \frac{1}{{16}}} \right)\]

\[ =  - 2\left[ {{{\left( {t - \frac{1}{4}} \right)}^2} - \frac{9}{{16}}} \right] = \frac{9}{8} - 2{\left( {t - \frac{1}{4}} \right)^2}.\]

Vì \[{\left( {t - \frac{1}{4}} \right)^2} \ge 0\] nên  \[ - 2{\left( {t - \frac{1}{4}} \right)^2} \le 0,\] do đó \[P \le \frac{9}{8}.\]

Dấu đẳng thức xảy ra khi \[t - \frac{1}{4} = 0,\] tức là \[t = \frac{1}{4}\] (thoả mãn).

Với \(t = \frac{1}{4},\) ta có \[\frac{1}{x} = \frac{1}{4},\] suy ra \[x = 4.\]

Vậy giá trị lớn nhất của \[M\] là \[\frac{9}{8}\] khi \[x = 4.\]