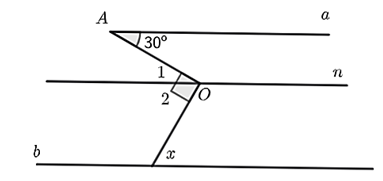
Cho hình vẽ bên, có \(Aa\) là tia phân giác của \(\widehat {xAn}\) và tia \(Bb\) nằm trong \(\widehat {mBy'}\) song song với tia \(Aa.\)
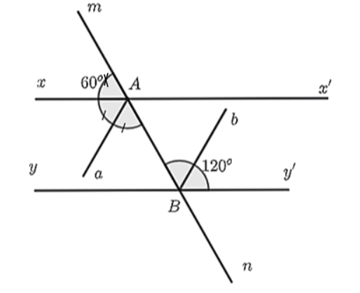
Cho hình vẽ bên, có \(Aa\) là tia phân giác của \(\widehat {xAn}\) và tia \(Bb\) nằm trong \(\widehat {mBy'}\) song song với tia \(Aa.\)

a) \(\widehat {xAm}\) và \(\widehat {mAx'}\) là hai góc kề bù.
b) \(\widehat {xAB} = \widehat {mAx'} = 120^\circ .\)
c) \[xx'\parallel yy'.\]
Quảng cáo
Trả lời:
a) Đúng.
Nhận thấy, \(\widehat {xAm}\) và \(\widehat {mAx'}\) là hai góc kề bù. Do đó, ý a) là đúng.
Suy ra \(\widehat {xAm} + \widehat {mAx'} = 180^\circ \) hay \(\widehat {mAx'} = 180^\circ - \widehat {xAm} = 180^\circ - 60^\circ = 120^\circ \).
b) Đúng.
Lại có, \(\widehat {x'Am} = \widehat {xAB} = 120^\circ \) (hai góc đối đỉnh). Do đó, ý b) là đúng.
c) Đúng.
Ta có \(\widehat {x'Am} = \widehat {ABy'} = 120^\circ \).
Mà hai góc ở vị trí đồng vị nên \[xx'\parallel yy'.\] Do đó, ý c) đúng.
d) Đúng.
Theo đề, \(Aa\) là tia phân giác của \(\widehat {xAn}\) nên \(\widehat {xAa} = \widehat {aAB} = \widehat {\frac{{xAn}}{2}} = 60^\circ \).
Mà \(Aa\parallel Bb\) nên \(\widehat {aAB} = \widehat {ABb} = 60^\circ \) (so le trong)
Suy ra \(\widehat {ABb} = \frac{{\widehat {ABy'}}}{2}\), đồng thời tia \(Bb\) nằm trong \(\widehat {mBy'}\).
Do đó, \[Bb\] là tia phân giác của \[\widehat {ABy'}.\]
Vậy nên ý d) là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
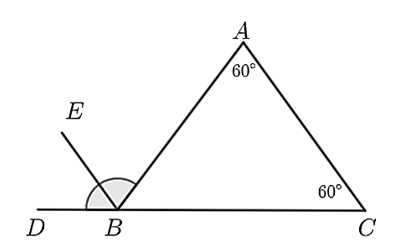
a) \[\widehat {DBA}\] là góc ngoài tại đỉnh \[B\] của tam giác \[ABC\].
b) Tam giác \[ABC\] là tam giác vuông tại \[B.\]
c) \[\widehat {DBA} = \widehat C + \widehat A\].
Lời giải
a) Đúng.
Nhận thấy \[\widehat {DBA}\] và \[\widehat {CBA}\] là hai góc kề bù. Do đó, \[\widehat {DBA}\] là góc ngoài tại đỉnh \[B\] của tam giác \[ABC.\]Vậy ý a) là đúng.
b) Sai.
Xét tam giác \[ABC\] có: \[\widehat A + \widehat B + \widehat C = 180^\circ \] (tổng ba góc trong tam giác)
Do đó, \[\widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right)\] hay \[\widehat B = 180^\circ - \left( {60^\circ + 60^\circ } \right) = 60^\circ \]. Do đó, tam giác \[ABC\] là tam giác đều.
Vậy ý b) là sai.
c) Đúng.
Vì \[\widehat {DBA}\] là góc ngoài tại đỉnh \[B\] của tam giác \[ABC\] nên ta có \[\widehat {DBA} = \widehat C + \widehat A\].
Vậy ý c) là đúng.
d) Đúng.
Có \[\widehat {DBA} = \widehat C + \widehat A = 60^\circ + 60^\circ = 120^\circ \].
Nhận thấy \[BE\] là phân giác của \[\widehat {DBA}\] nên \[\widehat {DBE} = \widehat {EBA} = \frac{{\widehat {DBA}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \].
Do đó, \[\widehat {EBA} = \widehat {BAC} = 60^\circ \].
Mà hai góc ở vị trí so le trong nên \[BE\parallel AC\].
Vậy ý d) là đúng.
Lời giải
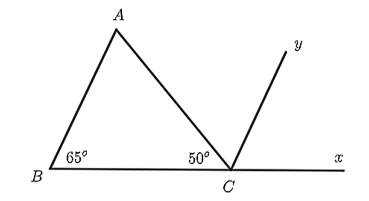
Vì hai tia \(Cx\) và \(CB\) đối nhau nên \(\widehat {xCB}\) là góc bẹt.
Ta có \(\widehat {ACB}\) và \(\widehat {ACx}\) là hai góc kề bù nên \(\widehat {ACB} + \widehat {ACx} = 180^\circ \) hay \(50^\circ + \widehat {ACx} = 180^\circ \)
Suy ra \(\widehat {ACx} = 180^\circ - 50^\circ = 130^\circ \).
Lại có tia \(Cy\) là tia phân giác của \(\widehat {ACx}\) nên \(\widehat {ACy} = \widehat {yCx} = \widehat {\frac{{ACx}}{2}} = 65^\circ \).
Vậy \(\widehat {ACy} = 65^\circ \).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
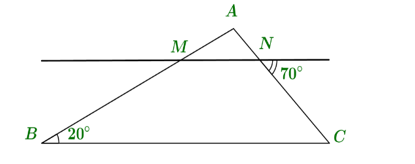
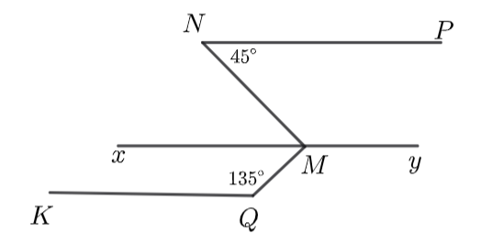
a) \[\widehat {NMx}\] và \[\widehat {QMx}\] là hai góc kề nhau.
b) \[\widehat {yMQ} = \widehat {KQM} = 135^\circ \] (hai góc đồng vị).
c) \[\widehat {QMx} = 45^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
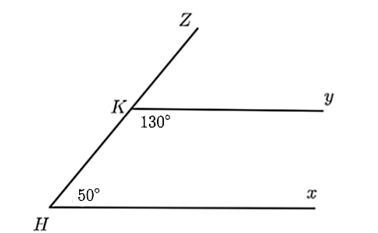
a) \(\widehat {zKy}\) và \(\widehat {yKH}\) là hai góc ở vị trí kề bù.
b) \(\widehat {zKy}\) và \(\widehat {KHx}\) là hai góc ở vị trí so le trong.
c) \(\widehat {zKy} = 50^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
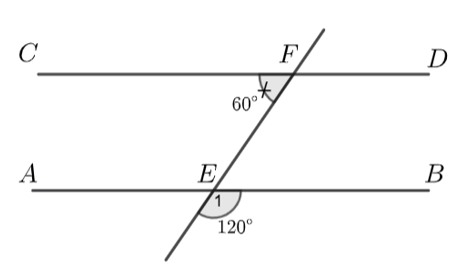
A. \(\widehat {BEF} = 60^\circ .\)
B. \(AB\parallel CD\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.