1) Cho \(\Delta ABC\) có \(AD\) là trung tuyến, trọng tâm \(G,\) đường thẳng đi qua \(G\) cắt các cạnh \(AB,\,\,AC\) lần lượt tại \(E,\,\,F.\) Từ \(B,\,\,C\) kẻ các đường song song với \(EF\) cắt \(AD\) lần lượt tại \(M,\,\,N.\) Chứng minh rằng:
a) \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\) b) \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1.\) c) \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
2) Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con dốc với đỉnh dốc tại điểm \[C\] (như hình vẽ).
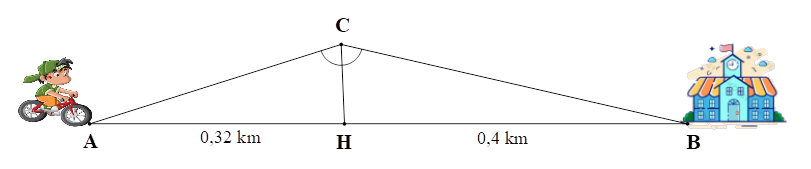
Điểm \(H\) là một điểm thuộc đoạn thẳng \[AB\] sao cho \[CH\] đường là phân giác \(\widehat {ACB},\) \[AH = 0,32{\rm{\;km}}\] và \[BH = 0,4{\rm{\;km}}.\] Biết bạn Hải đi xe đạp đến \[C\] lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h?
1) Cho \(\Delta ABC\) có \(AD\) là trung tuyến, trọng tâm \(G,\) đường thẳng đi qua \(G\) cắt các cạnh \(AB,\,\,AC\) lần lượt tại \(E,\,\,F.\) Từ \(B,\,\,C\) kẻ các đường song song với \(EF\) cắt \(AD\) lần lượt tại \(M,\,\,N.\) Chứng minh rằng:
a) \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\) b) \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1.\) c) \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
2) Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con dốc với đỉnh dốc tại điểm \[C\] (như hình vẽ).
Điểm \(H\) là một điểm thuộc đoạn thẳng \[AB\] sao cho \[CH\] đường là phân giác \(\widehat {ACB},\) \[AH = 0,32{\rm{\;km}}\] và \[BH = 0,4{\rm{\;km}}.\] Biết bạn Hải đi xe đạp đến \[C\] lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
1)
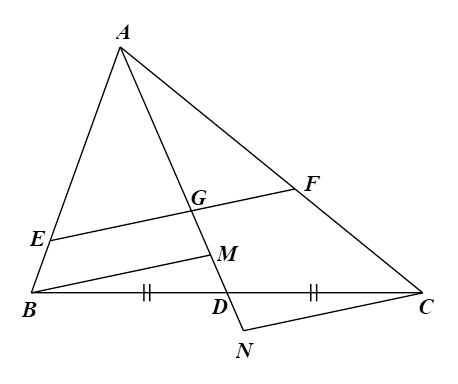
a) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\)
b) Xét \(\Delta DCN\) có \(BM\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}}.\)
Mà \(D\) là trung điểm của \(BC\) (do \(AD\) là trung tuyến của tam giác) nên \(DC = DB.\)
Do đó \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}} = 1,\) nên \(DM = DN.\)
Suy ra \(GM + GN = GM + GM + MN = 2GM + 2MD = 2GD.\)
Lại có \(G\) là trọng tâm \(\Delta ABC\) nên \(AG = 2GD.\)
Xét \(\Delta ACN\) có \(FG\,{\rm{//}}\,CN,\) theo định lí Thalès ta có: \(\frac{{CF}}{{AF}} = \frac{{GN}}{{AG}}.\)
Suy ra \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = \frac{{MG}}{{AG}} + \frac{{GN}}{{AG}} = \frac{{GM + GN}}{{AG}} = \frac{{2GD}}{{2GD}} = 1.\)
c) Xét \(\Delta ABM\) có \(EG\,{\rm{//}}\,BM,\) theo định lí Thalès ta có: \(\frac{{AB}}{{AE}} = \frac{{AM}}{{AG}}.\)
Xét \(\Delta ACN\) có \[FG\,{\rm{//}}\,CN,\] theo định lí Thalès ta có: \(\frac{{AC}}{{AF}} = \frac{{AN}}{{AG}}.\)
Suy ra \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = \frac{{AM}}{{AG}} + \frac{{AN}}{{AG}}\)\( = \frac{{AG + GM + AG + GM + MN}}{{AG}}\)
\( = \frac{{2AG + 2GM + 2MD}}{{AG}}\)\( = \frac{{2AG + 2\left( {GM + MD} \right)}}{{AG}} = \frac{{2AG + 2GD}}{{AG}}\)
\( = \frac{{2AG + 2 \cdot \frac{1}{2}AG}}{{AG}} = \frac{{3AG}}{{AG}} = 3.\)
Vậy \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)
2)
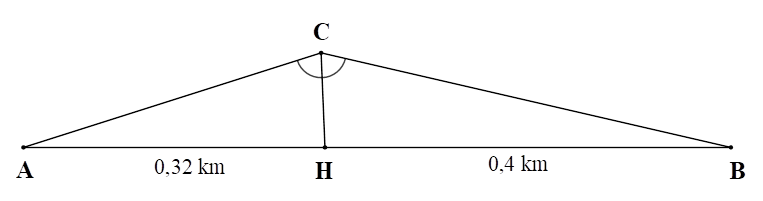
Thời gian để bạn Hải đi từ \[A\] đến \[C\] là: \[6\] giờ \[30\] phút \( - \,\,6\) giờ \[ = 30\] phút \[ = 0,5\] giờ.
Quãng đường mà bạn Hải đi từ \[A\] đến \[C\] trong \(0,5\) giờ với tốc độ trung bình lên dốc 4 km/h là: \[AC = {S_{A \to C}} = 4 \cdot 0,5 = 2\] (km).
Xét \(\Delta ACB\) có \[CH\] là đường phân giác của \(\widehat {ACB},\) nên ta có: \(\frac{{HA}}{{HB}} = \frac{{CA}}{{CB}}\) hay \(\frac{{0,32}}{{0,4}} = \frac{2}{{CB}}\) Suy ra \(CB = \frac{{0,4 \cdot 2}}{{0,32}} = 2,5\) (km).
Thời gian để bạn Hải đi hết quãng đường \(2,5\) km với tốc độ trung bình xuống dốc 10 km/h là: \(\frac{{2,5}}{{10}} = 0,25\) (giờ).
Như vậy, tổng thời gian bạn Hải đi từ \[A\] đến trường \[B\] là
\[0,5 + 0,25 = 0,75\] (giờ) \[ = 45\] (phút).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Do đường thẳng \[{d_1}\] đi qua điểm \(A\left( {1;1} \right)\) nên thay \[x = 1,{\rm{ }}y = 1\] vào hàm số \[y = mx - 2m - 2\] ta có:
\[1 = m \cdot 1 - 2m - 2\]
Do đó \[1 = m--2m--2\]
Suy ra \[m = --3.\]
Vậy với \[m = - 3\] thì đường thẳng \({d_1}\) đi qua điểm \(A\left( {1;1} \right).\)
b) Với \[m = - 3\], ta có đường thẳng \[{d_1}:{\rm{ }}y = - 3x + 4.\]
Suy ra hệ số góc của đường thẳng \[{d_1}\] là \[a = --3 < 0.\] Vậy góc \(\alpha \) là góc tù.
c) Để \({d_1}\) và \({d_2}\) cắt nhau thì \[m \ne 3 - 2m\] hay \[3m \ne 3\], suy ra \[m \ne 1.\]
Vậy với \(m \ne 0,m \ne \frac{3}{2},m \ne 1\) thì \({d_1}\) và \({d_2}\) cắt nhau.
Câu 2
A. \(\left( {2;0} \right).\)
B. \(\left( {0; - 6} \right).\)
C. \(\left( { - 6;0} \right).\)
D. \(\left( {0;2} \right).\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Hoành độ giao điểm của đồ thị hàm số bậc nhất \(y = 3x - 6\) với trục \(Oy\) là 0.
Do đó ta có \(y = 3 \cdot 0 - 6 = - 6\)
Vậy tọa độ giao điểm của đồ thị hàm số bậc nhất \(y = 3x - 6\) với trục \(Ox\) là \(\left( {0; - 6} \right).\)Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[0.\]
B. \[1.\]
C. \[2.\]
D. \[3.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. cắt nhau.
B. song song với nhau.
C. trùng nhau.
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{BD}}{{AD}} = \frac{{BE}}{{BC}}.\)
B. \(\frac{{BD}}{{AD}} = \frac{{BE}}{{EC}}.\)
C. \(\frac{{DE}}{{AC}} = \frac{{BC}}{{BE}}.\)
D. \(\frac{{AD}}{{AB}} = \frac{{BC}}{{EC}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập