Một cái mũ bằng vải của nhà ảo thuật có dạng hình trụ và với kích thước mô phỏng như hình vẽ.
a) Hãy tính tổng diện tích vải cần có để làm nên cái mũ đó (không tính phần viền, mép dán) (làm tròn kết quả đến phần trăm ).
b) Hãy tính thể tích phần có dạng hình nón của chiếc mũ đó (làm tròn kết quả đến phần trăm).
a) Hãy tính tổng diện tích vải cần có để làm nên cái mũ đó (không tính phần viền, mép dán) (làm tròn kết quả đến phần trăm ).
b) Hãy tính thể tích phần có dạng hình nón của chiếc mũ đó (làm tròn kết quả đến phần trăm).
Câu hỏi trong đề: Các dạng bài tập Hình trụ và hình nón lớp 9 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Bán kính hình trụ của cái mũ là \(r = \frac{{35 - 10 - 10}}{2} = \frac{{15}}{2}\;\left( {cm} \right)\).
Đường cao hình trụ của cái mũ là \(30\;cm\).
Diện tích xung hình trụ là: \({S_{xq}} = 2\pi rl = 2.\pi .\frac{{15}}{2}.30 = 450\pi \;\left( {c{m^2}} \right)\).
Diện tích vành mũ là: \({S_v} = \pi {\left( {\frac{{35}}{2}} \right)^2} - \pi {\left( {\frac{{15}}{2}} \right)^2} = 250\pi \left( {c{m^2}} \right)\).
Vậy tổng diện tích vải cần có để làm nên cái mũ đó (không tính phần viền, mép dán) là:
\(S = {S_{xq}} + {S_v} = 450\pi + 250\pi = 200\pi \approx \;628,32\left( {c{m^2}} \right)\).
b) thể tích phần có dạng hình nón của chiếc mũ là
\[V = \pi {r^2}h = \pi {\left( {\frac{{15}}{2}} \right)^2}.30 = \frac{{3375}}{2}\pi \approx 5301,44\left( {c{m^3}} \right)\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
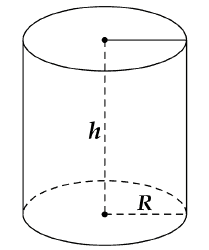
Vì ống hút hình trụ có bán kính đáy R = 0,4: 2 = 0,2 cm và chiều cao h = 18 cm nên diện tích xung quanh của ống hút là:
\[{S_{xq}} = 2\pi rh = 2\pi .0,2.18 \approx 22,608\left( {c{m^2}} \right)\]
Vậy khi thải ra môi trường, diện tích nhựa gây ô nhiễm cho môi trường do 100 ống hút này gây ra là\(100.{\rm{ }}22,608 = 2260,8\) cm2.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
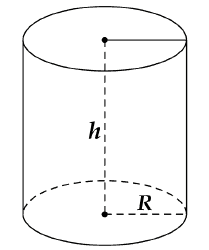
Vì hộp sữa hình trụ có chiều cao h = 12 cm và thể tích Vhộp = 192p cm3 nên:
\[\begin{array}{l}V = \pi {r^2}h\\192\pi = 12\pi {r^2}\\{r^2} = 16\\ \Rightarrow r = 4cm\end{array}\]
Vì hộp sữa hình trụ có \[r = 4cm\] và chiều cao h = 12 cm nên diện tích toàn phần của hộp sữa là:
\[{S_{tp}} = 2\pi r\left( {h + r} \right) = 2\pi .4\left( {12 + 4} \right) \approx 402,124\left( {c{m^2}} \right) \approx 0,04{m^2}\]
Chi phí sản xuất 10 000 vỏ hộp sữa là: \[0,04.10000.80000 = 32000000\] đồng
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập