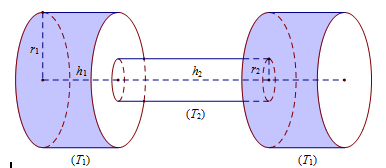
Tạo lập hình trụ có bán kính đáy \[r = 4\left( {cm} \right)\] và thể tích \[V = 224\pi \left( {cm} \right)\]
Tạo lập hình trụ có bán kính đáy \[r = 4\left( {cm} \right)\] và thể tích \[V = 224\pi \left( {cm} \right)\]
Quảng cáo
Trả lời:
Bước 1: Cắt hai miếng bìa có dạng hình tròn với bán kính \[r = 5\left( {cm} \right)\] (hình 1).
![Tạo lập hình trụ có bán kính đáy \[r = 5\left( {cm} \right)\] và chiều cao \[h = 8\left( {cm} \right)\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/5-1769740073.png)
Bước 2: Cắt một tấm bìa hình chữ nhật \[ABCD\] có cạnh \[h = 8\left( {cm} \right)\] và cạnh \[2\pi .r = 2\pi .5 \approx 31,4\left( {cm} \right)\] (hình 2).
![Tạo lập hình trụ có bán kính đáy \[r = 5\left( {cm} \right)\] và chiều cao \[h = 8\left( {cm} \right)\] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/01/6-1769740084.png)
Bước 3: Ghép và dán các miếng bìa vừa cắt ở bước 1, bước 2 (hình 3), ta được một hình trụ có bán kính đáy \[r = 5\left( {cm} \right)\]và chiều cao \[h = 8\left( {cm} \right)\] (hình 4).
![Tạo lập hình trụ có bán kính đáy \[r = 5\left( {cm} \right)\] và chiều cao \[h = 8\left( {cm} \right)\] (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2026/01/7-1769740107.png)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
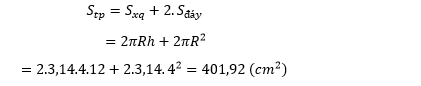
Lời giải
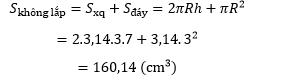
Vậy diện tích giấy để làm 100 hộp sữa chua là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.