Từ một tấm tôn hình chữ nhật kích thước \(50\,{\rm{cm}}\)x\(240\,{\rm{cm}}\), người ta làm các thùng đựng nước hình trụ có chiều cao bằng \[50\,{\rm{cm}}\], theo hai cách sau (xem hình minh họa dưới đây):
• Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
• Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu \({V_1}\) là thể tích của thùng gò được theo cách 1 và \({V_2}\) là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
Từ một tấm tôn hình chữ nhật kích thước \(50\,{\rm{cm}}\)x\(240\,{\rm{cm}}\), người ta làm các thùng đựng nước hình trụ có chiều cao bằng \[50\,{\rm{cm}}\], theo hai cách sau (xem hình minh họa dưới đây):
• Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
• Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu \({V_1}\) là thể tích của thùng gò được theo cách 1 và \({V_2}\) là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).

Quảng cáo
Trả lời:
Ở cách 1, thùng hình trụ có chiều cao \[h = 50\,{\rm{cm}}\], chu vi đáy \({C_1} = 240\,{\rm{cm}}\) nên bán kính đáy \({R_1} = \frac{{{C_1}}}{{2\pi }} = \frac{{120}}{\pi }\,\,{\rm{cm}}\). Do đó thể tích của thùng là \({V_1} = \pi R_1^2h\).
Ở cách 2, hai thùng đều có có chiều cao \[h = 50\,{\rm{cm}}\], chu vi đáy \({C_2} = 120\,{\rm{cm}}\) nên bán kính đáy \({R_1} = \frac{{{C_2}}}{{2\pi }} = \frac{{60}}{\pi }\,\,{\rm{cm}}\). Do đó tổng thể tích của hai thùng là \({V_2} = 2\pi R_2^2h\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi R_1^2h}}{{2\pi R_2^2h}} = \frac{1}{2}.{\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^2} = \frac{1}{2}.{\left( {\frac{{\frac{{120}}{\pi }}}{{\frac{{60}}{\pi }}}} \right)^2} = 2\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
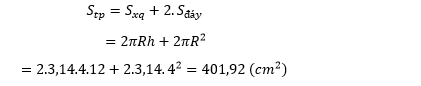
Lời giải
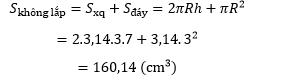
Vậy diện tích giấy để làm 100 hộp sữa chua là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.