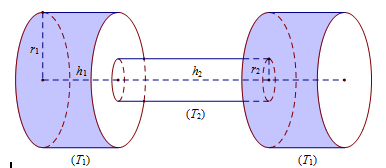
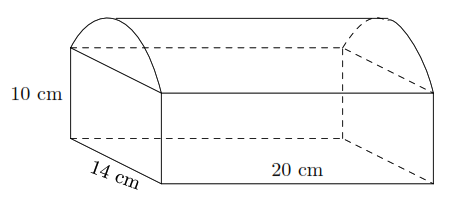
Một vật thể hình học có hình vẽ như hình bên. Phần trên là một nửa hình trụ, phần dưới là một hình hộp chữ nhật. Với các kích thước cho như hình vẽ. Vật thể này chứa tối đa bao nhiêu lít nước
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thể tích của vật thể là
\(V = {V_{hhcn}} + \frac{1}{2}{V_{tru}} = 14.20.10 + \pi {.7^2}.20 \approx 5878,8\,(c{m^3}) \approx 5,9\,(l)\)
Vậy vật thể chứa tối đa 5,9 lít nước
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
Nhắn tin Zalo
Hỏi bài tập