Cho hai biểu thức:
\(A = \frac{2}{{5.7}} + \frac{5}{{7.12}} + \frac{7}{{12.19}} + \frac{9}{{19.28}} + \frac{{11}}{{28.39}} + \frac{1}{{39.40}}\) và \[B = \frac{1}{{20}} + \frac{1}{{44}} + \frac{1}{{77}} + \frac{1}{{119}} + \frac{1}{{170}}\].
Chứng minh \(A > B\).
Cho hai biểu thức:
\(A = \frac{2}{{5.7}} + \frac{5}{{7.12}} + \frac{7}{{12.19}} + \frac{9}{{19.28}} + \frac{{11}}{{28.39}} + \frac{1}{{39.40}}\) và \[B = \frac{1}{{20}} + \frac{1}{{44}} + \frac{1}{{77}} + \frac{1}{{119}} + \frac{1}{{170}}\].
Chứng minh \(A > B\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Ta có: \(A = \frac{2}{{5.7}} + \frac{5}{{7.12}} + \frac{7}{{12.19}} + \frac{9}{{19.28}} + \frac{{11}}{{28.39}} + \frac{1}{{39.40}}\)
\( = \frac{1}{5} - \frac{1}{7} + \frac{1}{7} - \frac{1}{{12}} + \frac{1}{{12}} - \frac{1}{{19}} + \frac{1}{{19}} - \frac{1}{{28}} + \frac{1}{{28}} - \frac{1}{{39}} + \frac{1}{{39}} - \frac{1}{{40}}\)
\( = \frac{1}{5} - \frac{1}{{40}}\)\( = \frac{8}{{40}} - \frac{1}{{40}} = \frac{7}{{40}}\);
\[B = \frac{1}{{20}} + \frac{1}{{44}} + \frac{1}{{77}} + \frac{1}{{119}} + \frac{1}{{170}}\]
\[ = \frac{2}{{40}} + \frac{2}{{88}} + \frac{2}{{154}} + \frac{2}{{238}} + \frac{2}{{340}}\]
\[ = 2.\left( {\frac{1}{{5.8}} + \frac{1}{{8.11}} + \frac{1}{{11.14}} + \frac{1}{{14.17}} + \frac{1}{{17.20}}} \right)\]
\[ = 2.\frac{1}{3}.\left( {\frac{3}{{5.8}} + \frac{3}{{8.11}} + \frac{3}{{11.14}} + \frac{3}{{14.17}} + \frac{3}{{17.20}}} \right)\]
\[ = \frac{2}{3}.\left( {\frac{1}{5} - \frac{1}{8} + \frac{1}{8} - \frac{1}{{11}} + \frac{1}{{11}} - \frac{1}{{14}} + \frac{1}{{14}} - \frac{1}{{17}} + \frac{1}{{17}} - \frac{1}{{20}}} \right)\]
\[ = \frac{2}{3}.\left( {\frac{1}{5} - \frac{1}{{20}}} \right)\]\[ = \frac{2}{3}.\left( {\frac{4}{{20}} - \frac{1}{{20}}} \right)\]\[ = \frac{2}{3}.\frac{3}{{20}}\]\[ = \frac{1}{{10}}\].
Ta có: \(\frac{7}{{40}} > \frac{4}{{40}} = \frac{1}{{10}}\).
Do đó \(A > B\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: D
Ta có: \(\frac{{ - 7}}{{13}} \cdot \frac{6}{{11}} \cdot \frac{{13}}{7}\)\( = \frac{{\left( { - 7} \right).6.13}}{{13.11.7}}\)\( = \frac{{\left( { - 1} \right).6}}{{11}}\)\[ = - \frac{6}{{11}}\]
Vậy kết quả của phép tính là \( - \frac{6}{{11}}\).
Câu 2
Lời giải
Đáp án đúng là: B
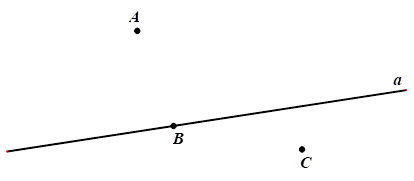
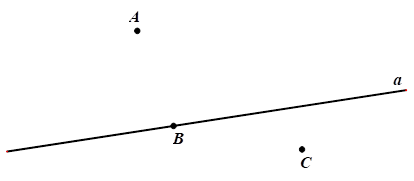
Trong hình vẽ, ta có
\[A \notin a;\,\,C \notin a;\,\,B \in a.\]
Do đó, khẳng định \[C \in a\] là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.