Cho \[A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \cdot \cdot \cdot \cdot \cdot + \frac{1}{{{{2012}^2}}} + \frac{1}{{{{2013}^2}}}\]. Chứng tỏ \[A < 1\].
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Ta có \[A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \cdot \cdot \cdot \cdot \cdot + \frac{1}{{{{2012}^2}}} + \frac{1}{{{{2013}^2}}}\].
Đặt \(B = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ....... + \,\frac{1}{{2012.2013}}\).
Ta có vì \[2 > 1\] nên \[2\,\,.\,\,2 > 1\,\,.\,\,2\].
Suy ra \(\frac{1}{{{2^2}}} = \frac{1}{{2.2}} < \frac{1}{{1.2}}\);
Tương tự:
\(\frac{1}{{{3^2}}} = \frac{1}{{3.3}} < \frac{1}{{2.3}}\);
….
\(\frac{1}{{{{2012}^2}}} = \frac{1}{{2012.2012}} < \frac{1}{{2011.2012}}\);
\(\frac{1}{{{{2013}^2}}} = \frac{1}{{2013.2013}} < \frac{1}{{2012.2013}}\).
Do đó \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \cdot \cdot \cdot \cdot \cdot + \frac{1}{{{{2012}^2}}} + \frac{1}{{{{2013}^2}}} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + ....... + \frac{1}{{2011.2012}} + \,\frac{1}{{2012.2013}}\).
Suy ra \[A < \;B\].
Mà \(B = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ....... + \,\frac{1}{{2012.2013}}\)
\( = \frac{{2 - 1}}{{1.2}} + \frac{{3 - 2}}{{2.3}} + ... + \frac{{2012 - 2011}}{{2011.2012}} + \frac{{2013 - 2012}}{{2012.2013}}\)
\( = \frac{2}{{1.2}} - \frac{1}{{1.2}} + \frac{3}{{2.3}} - \frac{2}{{2.3}} + ... + \frac{{2012}}{{2011.2012}} - \frac{{2011}}{{2011.2012}} + \frac{{2013}}{{2012.2013}} - \frac{{2012}}{{2012.2013}}\)
\[ = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{2012}} - \frac{1}{{2013}}\]\( = 1 - \frac{1}{{2013}} < 1\).
Do đó \[B < 1\] nên \[A < B < 1\].
Vậy \[A < 1\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

a) Vì điểm \[C\] nằm giữa hai điểm \[A\] và \[B\] nên \[AC + CB = AB\].
Suy ra \[AC = AB - CB = 5 - 3 = 2\] (cm).
Vậy \[AC = 2\] cm.
b) Trên tia đối của tia \[BA\] lấy điểm \[D\] sao cho \[BD = 2\] cm.
Vì điểm \[B\] nằm giữa hai điểm \[C\] và \[D\] nên \[CB + BD = CD\].
Suy ra \[CD = 3\;\; + \;2\; = \;5\] (cm).
Mà \[AB = 5\] cm nên \[AB = CD\].
Lời giải
Trục đối xứng của mỗi hình được biểu diễn như hình vẽ.
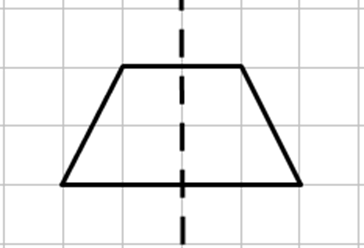
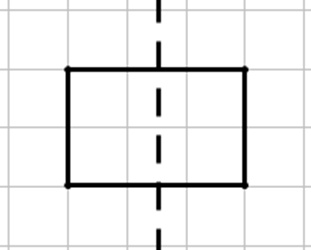
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Quan sát hình vẽ và cho biết tia đối của tia \[AB\] là tia (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid2-1770192536.png)