Câu hỏi:
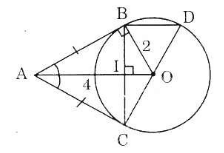
12/07/2024 43,534Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
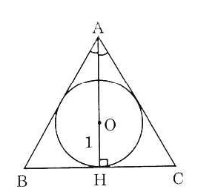
Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
Lời giải
- Chọn D.
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Nhắn tin Zalo
Trương Huyền
Giúp e vs ạ