Câu hỏi:
13/07/2024 1,604Cho hai đường tròn (O; R) và (O'; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO'. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; r) theo thứ tự C và D (khác A).
Chứng minh rằng AC = AD.
Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Kẻ OM ⊥ AD.
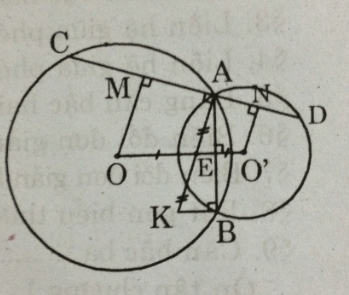
Theo tính chất đường kính vuông góc với một dây, ta có: MA = MC
Tương tự, kẻ O'N ⊥ AD => NA = ND.
Ta có:
Vậy tứ giác OMNO' là hình thang vuông.
Ta còn có: IO = IO' (gt) và IA // OM
Do đó IA là đường trung bình của hình thang OMNO'.
=> AM = AN hay 2AM = 2AN
Hay AC = CD (đpcm)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Tiếp tuyến với đường tròn là đường thẳng chỉ có một điểm chung với đường tròn.
- Tiếp tuyến với đường tròn thì vuông góc với bán kính đi qua tiếp điểm.
- Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua tiếp điểm ấy thì đường thẳng ấy là một tiếp tuyến của đường tròn.
- Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
a) Điểm đó cách đều hai tiếp điểm.
b) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
c) Tia kẻ từ tâm qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Lời giải
Gọi G là giao điểm của AH và EF
Tứ giác AEHF là hình chữ nhật => AH = EF
Do đó EF là tiếp tuyến của đường tròn (I)
Tương tự, EF là tiếp tuyến của đường tròn (K)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải