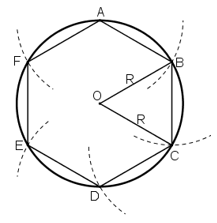
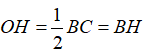Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
Câu hỏi trong đề: Giải Toán 9 phần Hình học Tập 2 !!
Quảng cáo
Trả lời:
* Vẽ lục giác đều nội tiếp (O; R) :
+ Lấy điểm A trên (O ; R).
+ Vẽ cung tròn (A; R) cắt (O; R) tại B và F => AB = AF = R
+ Vẽ cung tròn (B; R) cắt (O; R) tại C ( khác A) => BC = R
+ Vẽ cung tròn (C; R) cắt (O; R) tại D ( khác B) => CD = R
+ Vẽ cung tròn (D; R) cắt (O; R) tại E ( khác C)=> DE = R
ABCDEF là lục giác đều cần vẽ.
* Tính cạnh: AB = BC = CD = DE = EF = FA = R.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
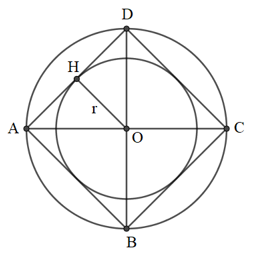
Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒
Xét tam giác vuông OHB có: r2 + r2 = OB2 = 22 ⇒ 2r2 = 4 ⇒ r2 = 2 ⇒ r = √2(cm)
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Lời giải
Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.